Shikaku

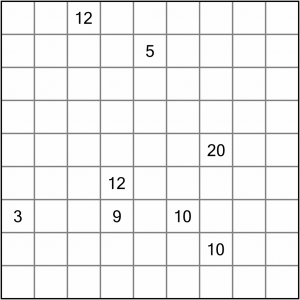
This is the puzzle we’re going to solve. It’s an easy level 1 puzzle – just enough of a challenge to show some solving techniques in action.

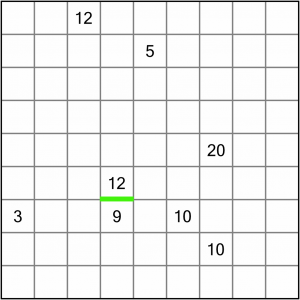
There are a couple of places we could start, but the easiest line to draw in is this one between the 12 and 9. No region can contain two numbers, so there has to be a division here. We don’t know where (or if) that line will extend yet, but it gives us something of a starting point. 

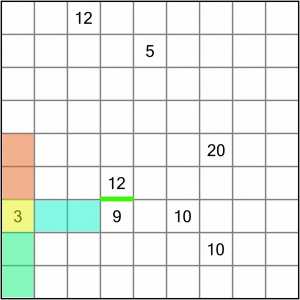
Let’s turn our attention to this 3. Because it’s on an edge, it’s more constrained than numbers in the middle of the board.

There are three ways we can draw a region of three squares that incorporate this number: we could go upwards (as shown by the orange area), or we could go sideways (blue) or downwards (green). To work out which way to go, we need to look at the neighbouring numbers that will affect the squares nearest the 3.

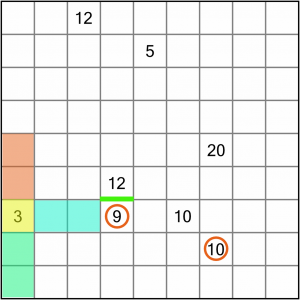
This 9 and 10 are of most interest. Why? Well, consider the possible scenarios: If we extended our 3 region into either the orange or blue squares, that would leave the green ones empty. Every square must be part of a numbered region when the puzzle is complete, so those green squares would have to join another region. The trouble is that neither the 9 region or the 10 region (the two closest) could be drawn in such a way as to include those green squares. 

Therefore, our 3 region must extend into the green squares, because that’s the only way to incorporate them into any region on the board.

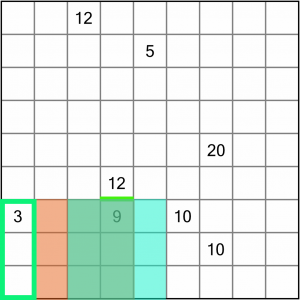
We can use the same logic to work out how to complete our partially drawn region around the 9. Given the 3 to the left, the 12 above, and the 10 to the right, we either have to draw around the orange region or the blue one. If we draw around the blue one, that’s going to leave three orphaned squares between the 9 region and the 3 region – squares that cannot be incorporated into any other region.

Therefore, we have to draw around the orange region for the 9.

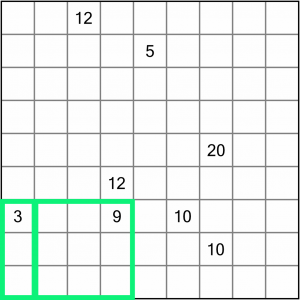
If we turn our attention to the two 10s, there’s only one way to draw a region around the bottom one because of the constraints imposed by the top 10 and the 20 higher up. We’ll draw that in next.

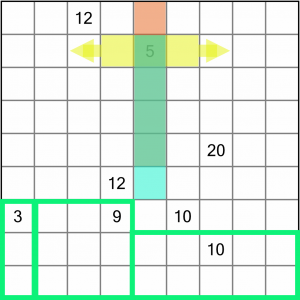
Now let’s look at the 5. It’s an odd number, and as it’s not divisible by three, it means we have to draw its region as a straight line. That limits the placement options considerably. We can either draw it vertically (the orange or blue regions), or horizontally (the yellow region, which could extend in either direction). 

The answer, once again, comes from working out how we would fill any remaining squares. If we went with the yellow region, or the blue one, we’d be leaving a single empty square above the 5. That square could not be used by the top 12 (because the board is only 9 squares wide), and neither could it be used by the 20 (because regions must be rectangular or square, they cannot be odd shapes that poke out to fill holes!) 

So our only option here is to incorporate that top square into the 5, which means we have to draw around the orange region.

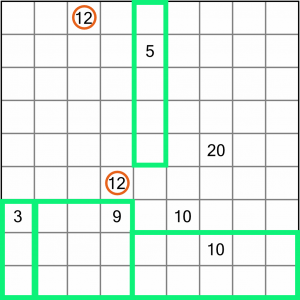
These two 12s are now easy to work out. They have twenty-four squares between them, so we just have to divide them in two. There’s no other way to draw two regions of twelve in this area.

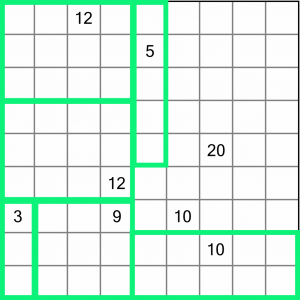
That leaves us with the 10 and the 20, and it should be pretty easy to work out how to divide those.

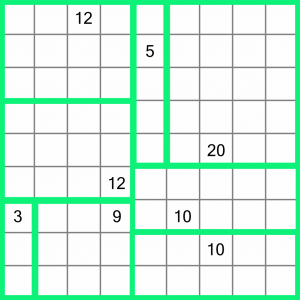
There, all done! As I said at the start, this was an easy puzzle. But don’t worry, they get a lot more complicated than that. Ready to try some yourself? Read on for some free puzzles to download, and details of where you can get more.