Sudoku From Scratch 3

Part Three - Speeding Up

In part one of this tutorial we began by looking at the basics of sudoku, using smaller than normal puzzles. Part two took us through using racks and stacks to solve 1-star level full size puzzles. Now it’s time to ramp things up to the next level - literally.

We’re going to look at a 2-star grid and learn a couple of techniques that will help you solve puzzles faster, and prepare you for even higher-level puzzles along the way.

If you’ve arrived here without any knowledge of sudoku, I’d highly recommend going back and covering those earlier sections first - everything here will make a lot more sense that way.

Levelling Up

Here’s a 2-star puzzle, taken from our Pocket Sudoku — Classic range:

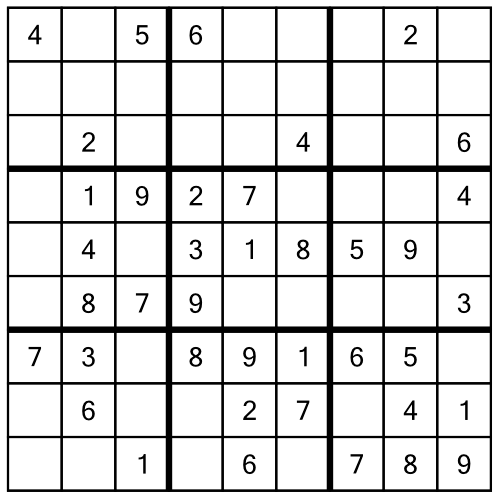
If you want to follow along yourself, you can download this grid to print out at home here.

A quick glance at the puzzle tells us there aren’t any easy single free cells to fill in - every row, column, and block has at least two empty cells. So we begin by working the racks and stacks. This time I’m going to do the racks first, because why not? There’s no right or wrong way to attack a sudoku puzzle.

Working across the top rack, we can fill in a 2 and a 4. When we get to the 6, there are two possible cells it could go in:

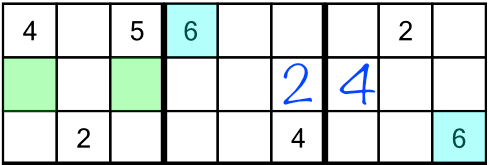
We could move on and look for the next number — it’s what we did back in part two of this tutorial in situations like this. But there’s a better way. Instead, we will write a tiny little number 6 in both the candidate cells, like this:

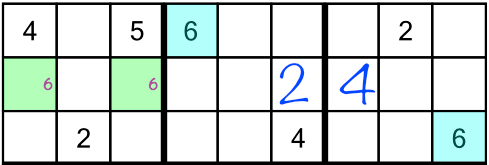
You’re probably wondering how this will help. Don’t worry, we’ll come on to that in a bit. First though, here’s some sudoku etiquette about how to write in little numbers. It’s best to always write them in the ‘correct’ place within a cell, because as we work through the puzzle we may end up putting more than one little number in a cell. Just jotting them down willy nilly will make our puzzle messy and hard to read. It’s better to have a system. To figure out where to write little numbers, just imagine the cell is filled with all the possible values, like this:

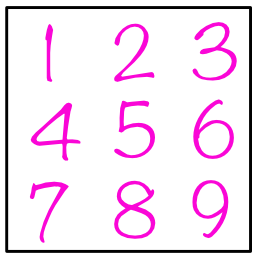
Sticking to this convention really makes working with the puzzle easier. By the way, it’s best to use pencil for solving sudoku puzzles because later you’ll want to erase the little numbers. It’s also good to have cells big enough to put several little numbers in without having to write microscopic digits. It’s why all Puzzle Genius sudoku books have generous sized grids - even our popular Pocket Sudoku range.

Back to our puzzle. There’s nothing more we can do with the top rack, so we move on to the middle one. Straight away we see that we have two candidate slots for the 1, so we can write in two little numbers:

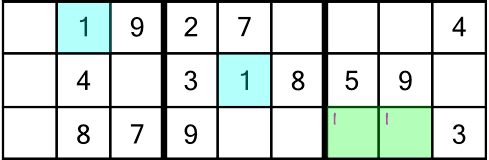
Working through the rack we can fill in the 3, 4, 7 and 8. This is what the grid looks like so far:

On to the third rack. The first opportunity we have to write anything in is the number 8. Again we have two candidate cells. We write in the little numbers, like this:

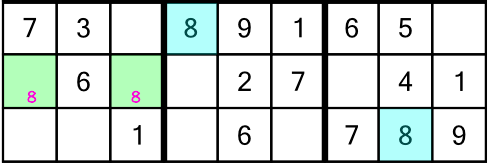
Now look what happens when we reach the number 9:

There’s a 9 in the middle block and top row (of the third rack), and there’s a 9 in the third block and bottom row. Logic tells us we have to put a 9 in the first block and middle row of the rack. There are two empty cells to consider, but one of them is out of bounds because there’s already a 9 in the column that cell is in. That leaves just one candidate cell, and it already has a little number 8 inside it. Remember, those little 8s are there to tell us one of the two cells must contain a number 8. When we write our 9 into the green cell (the only place it can go), we are ruling out the possibility of an 8 going in there:

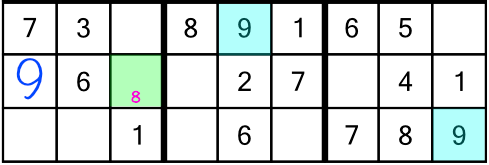
Now the only place left to put our 8 is the one remaining cell with a little 8 in it. Writing in the little numbers earlier meant we got to solve two cells in one go! 

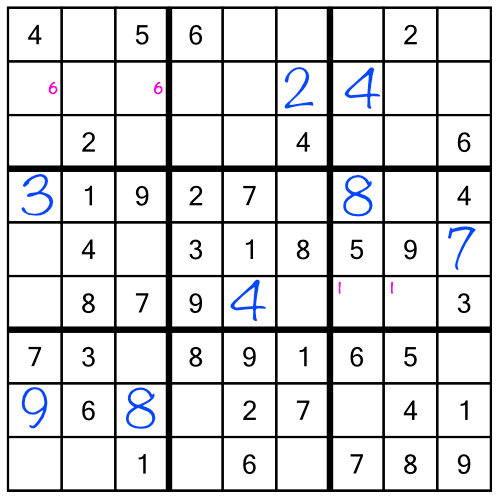
We would have found the 8 eventually, even without the little numbers. Our second tour through the racks — after we had worked through all the stacks — would have shown us where to put it. But doing it this way means we got to fill it in much earlier, saving us time and potentially making it easier to work through the stacks, because every completed cell makes the puzzle a little bit easier.

There are more benefits to using little numbers, and we’re going to cover one of those right now, as well as learning another technique that can speed up our sudoku solving powers!

Matching Pairs & Repercussions

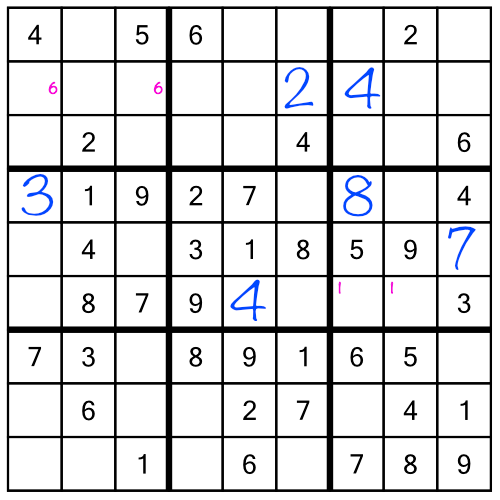
Let’s continue with our example puzzle. I’ve gone ahead and worked through the first stack, and the middle stack as far as the number 8. This is what the grid looks like so far:

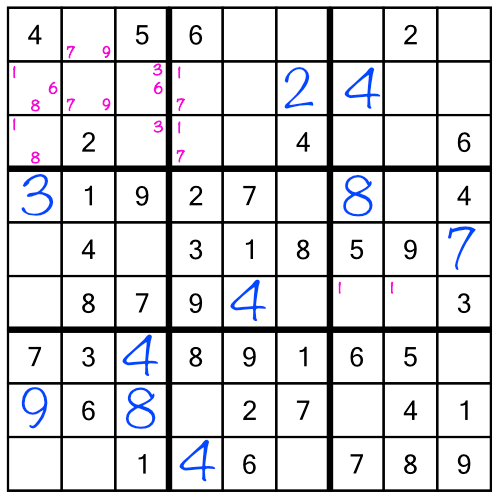
It’s starting to get a bit crowded - but don’t worry, all those little numbers are going to be a great help. Starting right now, when we add in the number 9 in the middle stack:

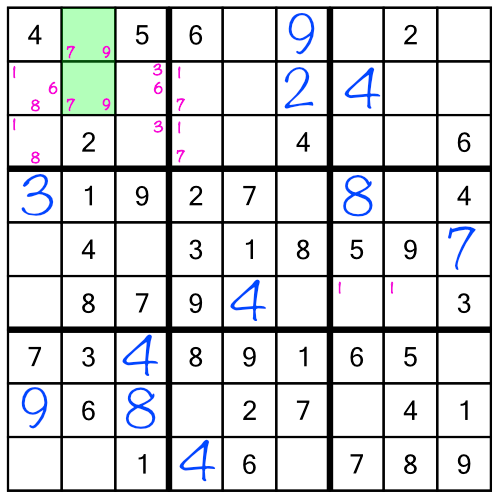
Looking back at the top left block, we notice the green cells both contain a little 7 and a little 9. When two cells in the same row, column, or block, contain two — and only two — little numbers, that tells us that they can only hold one of those two numbers. In other words one of those green cells must be a 7, and one must be a 9. There are no other numbers that could go there. And now that we’ve just filled in that 9 in the top row (middle stack), we’ve ruled out the possibility of the top green cell holding a 9!

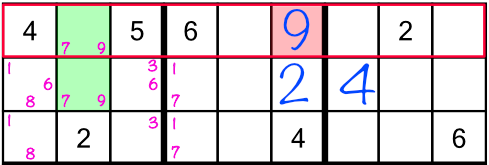
The repercussion of filling in the 9 in the top block of the middle stack is that now we know which green cell holds the 7 (the top one) and which holds the 9 (the bottom one):

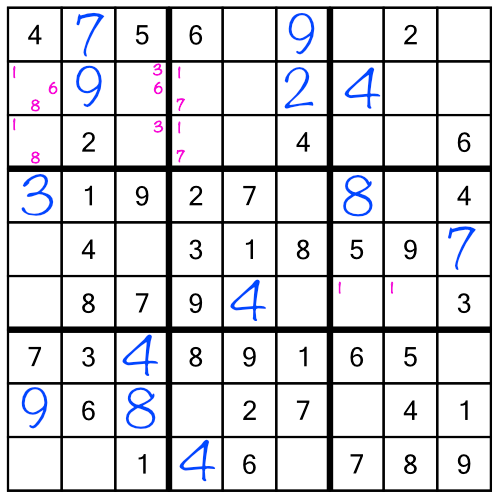
Repercussions are an amazing way to solve puzzles more quickly. The technique is simple: every time we fill in a cell definitively (that is to say with a full size number, not a little number), we look at the puzzle to see if that number helps us solve any other cells. The repercussion of filling in the 9 in the middle stack was that we could solve the 7 and 9 in the left stack.

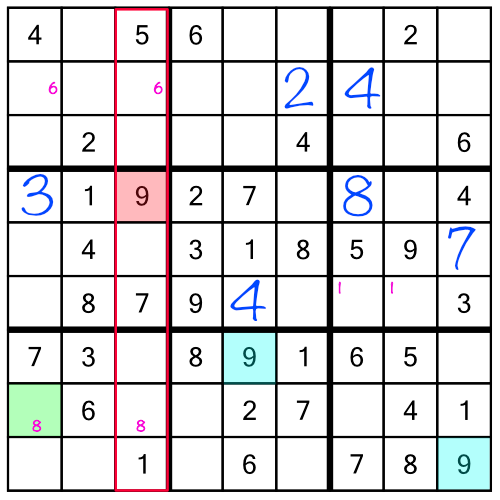
Before we move on working to the last stack, we can see if the 7 and 9 we just solved have any repercussions themselves

The 7s in the left stack are already all solved, and we don't have enough information to solve the 7s in the rack. But guess what? The new 9 means we can solve the third 9 in the top rack:

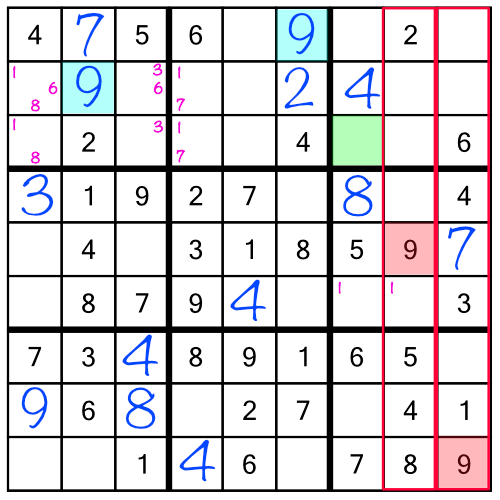
Now we've solved all the 9s in the puzzle. But that’s not the only repercussion. The 7 and 9 we added earlier have given us a single free cell in a column:

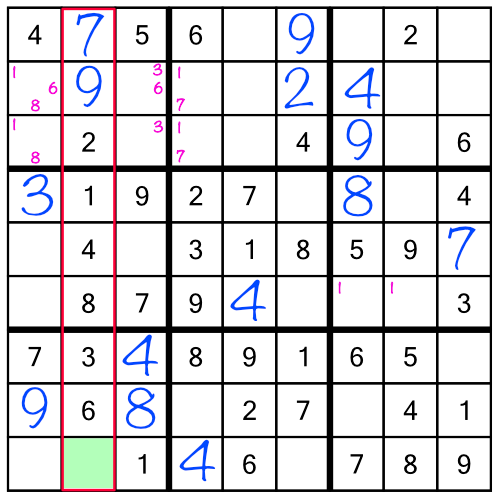
Filling it in with the number 5 gives us three more repercussions:

1. A single free cell in a block (green square, below).
2. A missing 5 in the left stack (yellow square).
3. A missing 5 in the bottom rack (purple square).

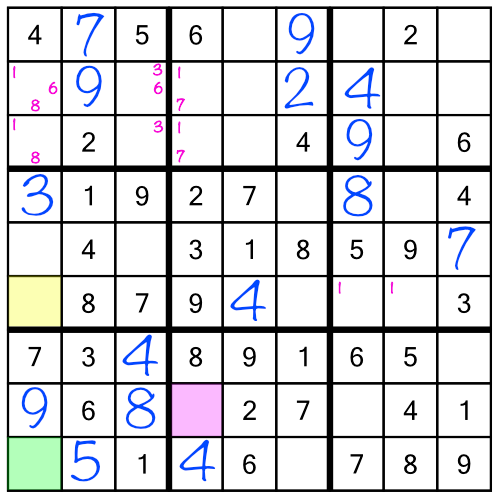
Filling in those numbers in turn gives new repercussions, and so on as the empty squares fall like dominoes. In fact, just by following the repercussions, we can solve the whole puzzle! We don’t even have to work through the final stack, and we certainly don’t need to work through the racks a second time.

Why not try and complete the rest of the puzzle yourself? When you are ready, you can download the solution here.

Wrapping Up

You now have enough techniques under your belt to solve 1 and 2-star puzzles, and with a bit of effort some harder ones too. There are plenty more techniques to discover though, and filling in those little numbers is key to making many of them work.

If you want to practice solving 2 star puzzles, we’ve put together some 2-star puzzles you can download and print out below, as well as the solutions to check your answers. And of course, we have a full range of high-quality sudoku books, including our popular A Year of Sudoku - with a new puzzle every day for a year.