If you’ve never played sudoku but want to get started, or if you’ve ever looked at a sudoku grid and found it intimidating or impenetrable, then you’ve come to the right place! This tutorial series assumes zero knowledge of the popular puzzle game. We’ll take you from scratch to being able to solve most puzzles up to intermediate level.
Sudoku is great fun, and is actually really easy to learn. It’s a good way to relax, to keep your mind sharp, and can be the perfect distraction from the difficult times we find ourselves in.
Contrary to popular belief, sudoku is not a mathematical puzzle. That it uses numbers is almost incidental. The numbers are just symbols, and in fact any kind of symbols can be used. Some kids sudoku grids use shapes or icons. Some sudoku puzzles use letters (these are usually called wordoku). Numbers are by far the most common symbol used in sudoku though, so that’s what we will stick with here.
The aim of the game is very straightforward: to find all the missing numbers in a partially filled grid of numbers.
To get started, we’re going to begin with a smaller than usual grid of numbers. It makes it easy to grasp the rules. What’s that, you say? What are the rules? Great question!
The rules of sudoku are encapsulated in its name, which comes from the Japanese Sūji wa dokushin ni kagiru, which means the numbers must be single. In sudoku, each number in a grid can only appear once in each row, column, and block.
Before we go any further, let’s look at what a grid looks like, and explain some of that terminology.
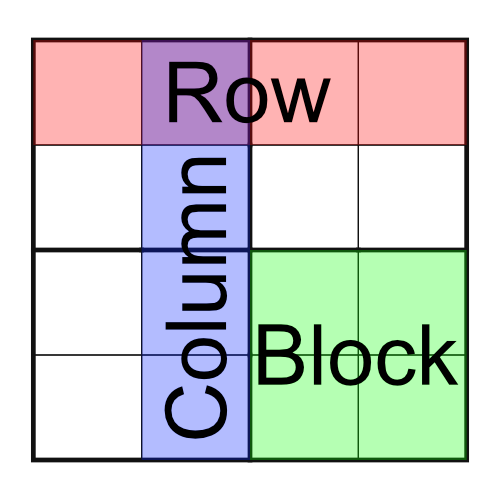
Here's an empty sudoku grid. We call this a 4x4 grid because it’s four cells across and four down. Small grids like this are great for kids.
Note: If you have kids who you think would enjoy sudoku, we recommend Amelia Baker’s excellent Sudoku For Kids series. It starts with small grids like this and works up to full size ones, with fun tutorials along the way. It’s all wrapped up in a beautifully decorated book that kids will love.
The grid has four rows (each comprising four cells), four columns (of four cells), and four blocks - also made up of four cells. Some sudoku designers refers to blocks as boxes regions, or if they want to get really fancy, nonets. At Puzzle Genius we prefer to stick with calling them blocks because, well, they’re kind of blocky.
Here’s a 4x4 grid with some numbers filled in:

The aim of the game of sudoku is to fill in the empty cells with the missing numbers. We can always do this with logic - there’s no need to guess. In fact, guessing is very bad and should never be part of solving a sudoku puzzle. That’s because if we guess at the contents and get it wrong, we won’t necessarily know until we are much further into the puzzle. By the time we realise something is wrong, we won’t know where our mistake occurred and the only way forward would be to start over from the beginning.
Remember that sudoku comes from the Japanese for the numbers must be single? That means that:
Armed with the numbers already present, and these simple rules, we can solve the puzzle.
With a tiny grid like this, the logic to solve the puzzle is almost self-explanatory. But let’s lay it out there anyway, because making sure we understand the basics means we’ll have a good foundation for solving bigger, more complex grids.
The easiest place to start is with a part of the grid that’s already almost complete. Looking back at our example, which is super-simple, there are a few places we could begin. Let’s take the highlighted column which only has one number missing:
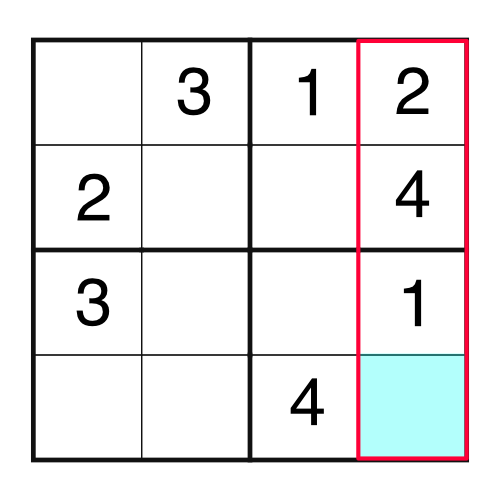
Given that column already has a 1, a 2, and a 4, the missing number is a 3. It’s the only number that can go in the blue square. We can write the 3 like this:
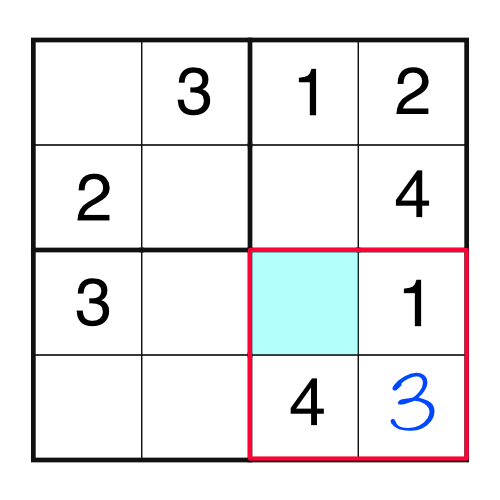
Now we have a block that’s only missing one number - the 2. Writing it in makes something interesting happen:
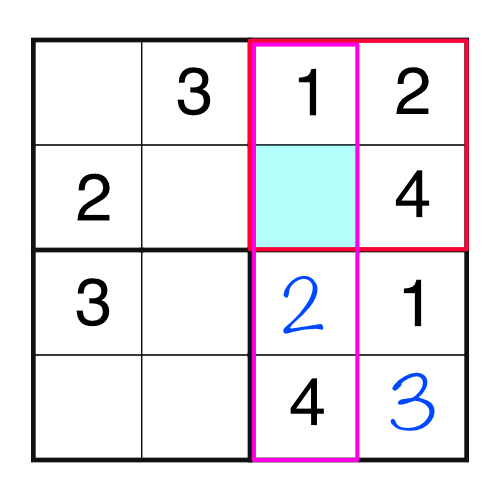
Look at that - there’s a block and a column that are both missing the same number. Fortunately they are missing the same number - the 3. If they were missing different numbers we would know we have a problem somewhere, because we’ve only got space to put one. Here’s what the grid looks like now:
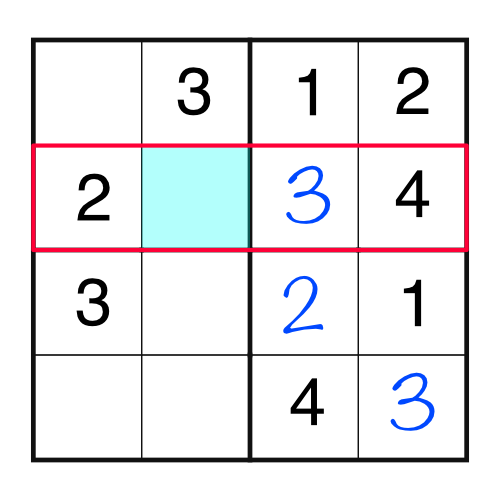
The next number is a 1:
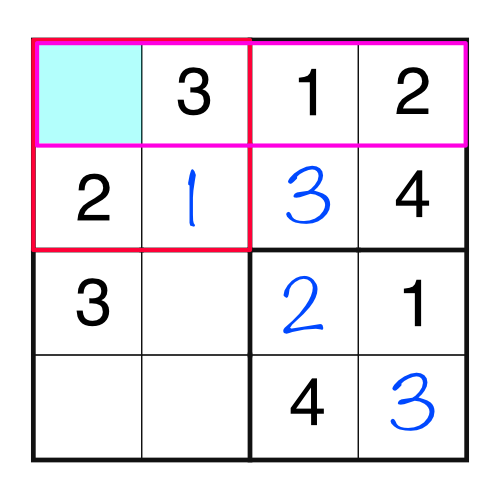
That gives us a block and row with the same empty cell, which has to be a 4.
It’s easy to keep filling in the single missing number each time until the whole grid is filled in. This is what the final solution looks like:

This example took one route to solving the puzzle, but it wasn’t the only route. There are no rules that say we had to start with the right-most column. It would have been just as easy to start with the top row, or the top-right block. In a puzzle this simple it’s possible to start in almost any cell. There’s no right or wrong way to proceed.
The sudoku puzzle has been completed, but are we sure we got the result right? Checking it is easy - we just have to apply the rules of sudoku to each row, column, and block. Working top to bottom, we can read off each row to make sure that they all contain the numbers 1-4 once and only once. Then we can work left to right doing the same for the columns. Finally we can triple check everything is hunky-dory by verifying each of the blocks also contains each number once and only once.
Sales pitch alert! Checking 4x4 puzzles takes seconds. Checking regular sudokus, which are 9 cells by 9 cells, takes longer. That’s why every Puzzle Genius puzzle book contains complete solutions at the back, to make it much faster to check your results.
The example we’ve just looked at was unusually easy. If every sudoku was that simple, the game would be very boring indeed. Let’s look at a more realistic puzzle, though we’ll stick with a 4x4 grid for this introductory tutorial.

This time there are no rows, columns, or blocks that are missing only one number. The best we can do is the block on the top left, which is missing two.
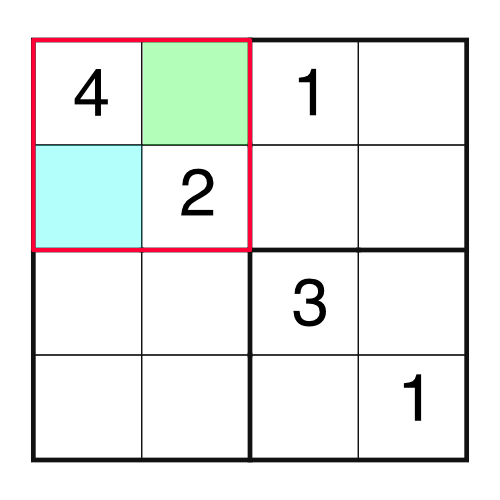
Logic is our friend. We have a 4 and a 2 in the block, which means we are missing a 1 and a 3. Which one goes in which empty cell? It’s easy enough to work out by considering other parts of the grid. For example, if we were to consider the top row, we would notice this:
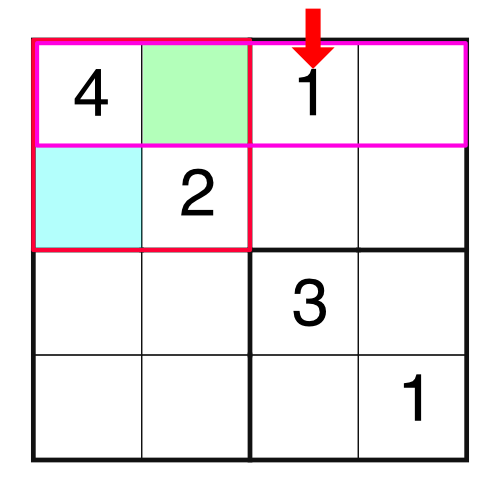
There is already a 1 in the top row, and we know we can’t put the same number into a row twice. That means we can’t put a 1 into the green square - we’d be breaking the rules. Therefore the only place the 1 can go in our highlighted block is the blue square.
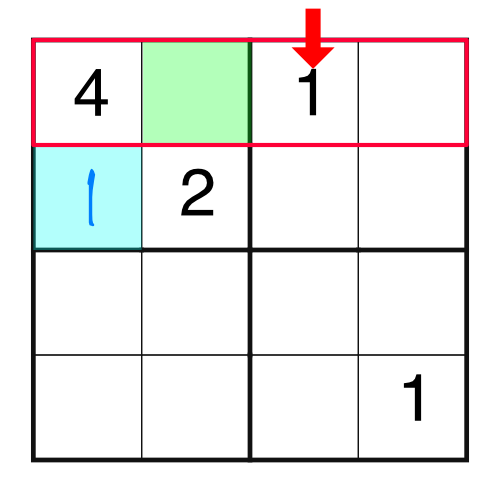
Now that block is only missing a 3, so that’s what goes in the green square.
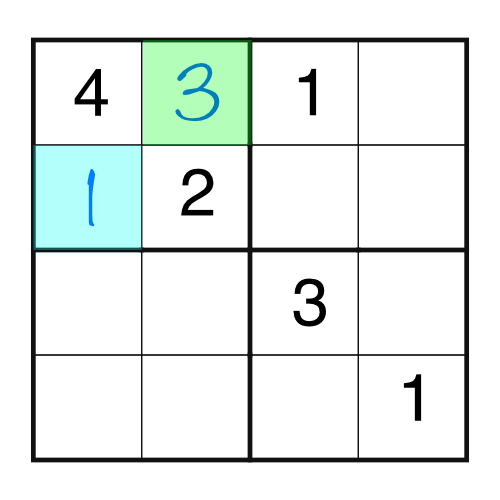
That little bit of login has opened up the puzzle. By filling in single missing cells we get to this stage.

At first glance, an entirely empty block might be difficult to solve. But it’s only a problem if we consider the block in isolation. Taking into account the rows and columns makes it a doddle.
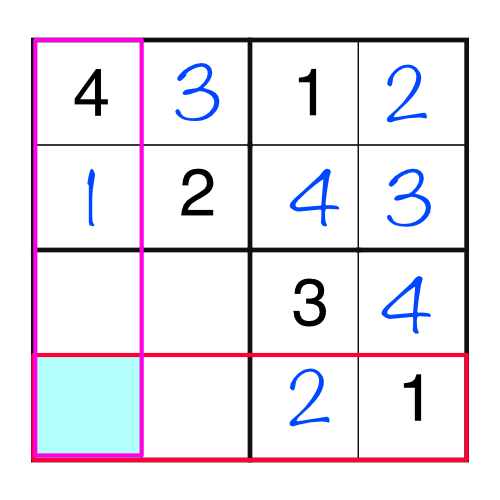
By looking at the intersection of the row and column highlighted, it’s obvious there’s only one number that can go in there. We can’t put a 4 or a 1, because they are already in the column, and we can’t put a 1 or a 2, because they are already in the row, so we’re only left with a 3.
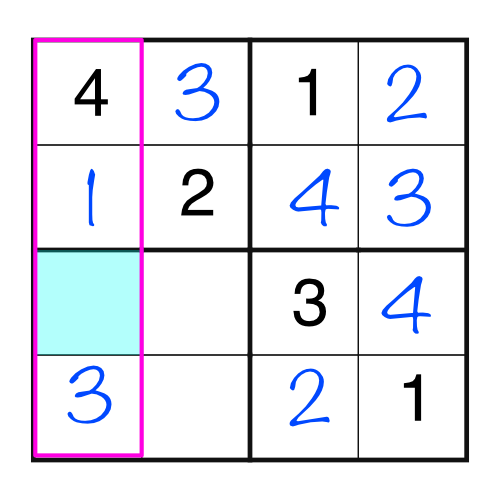
Once again, that simple logical leap has opened up the puzzle, and the remaining three cells are easy to fill in.

This introduction might be over-simplified, but it has been designed to give you the basis of logic required to solve sudoku puzzles.
Bigger puzzles, like those you’ll find in our books, can be solved with the same principles, although harder puzzles need some extra techniques. You’ll find lots of more advanced methods in the pages of this site.
In part two of this series we’ll look at regular sized sudoku, and introduces some helpful tricks you can use to solve puzzles up to intermediate level.
If you’d like to practice the very basics first though, we’ve put together a page of 4x4 puzzles below that you can print out.
4x4 Sudoku Practice — Solutions
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.