Calcudoku, which is sometimes also called Mathdoku and KenKen, is a mathematical and logic puzzle based on Sudoku. It’s played on various grid sizes, usually from 4x4 to 9x9, though it can go even larger.
The size of the grid dictates the numbers you’ll use to fill out the puzzle. For instance, in a 4x4 Calcudoku you'll use the numbers 1 to 4, and in a 6x6 you'll use the numbers 1 to 6.
Here’s an example of a small Calcudoku puzzle:
The objective of Calcudoku is to fill the grid with numbers according to the following rules.
Here’s what the earlier example puzzle looks like when completed:
Because Calcudoku shares similar rules to Sudoku, we highly recommend becoming familiar with solving Sudoku before moving on to this puzzle. As you begin to solve cells in a Calcudoku grid, you can use many regular Sudoku techniques to help you solve the rest of the puzzle. Indeed, in anything beyond the most basic puzzles, you’ll need to use Sudoku techniques. You can find our complete three-part Sudoku tutorial here.
Clue numbers in a Calcudoku puzzle are usually a number followed by a mathematical operator (e.g., ‘12x’ or ‘3-’), in which case the specified calculation must be performed on the numbers that are entered in the block. If a clue number is shown without an operator in anything other than a single cell, you’ll have to work out the calculation as well as the numbers, or use other Sudoku techniques to fill those cells without without worrying about the calculation part.
The puzzles we publish use a variety of mathematical operators. Our kids puzzles usually only include additions, but as the difficulty level increases, so do the possible operators.
A well-designed Calcudoku puzzle (such as those we publish) has only one unique solution, and it can be reached through logical deduction. There is never any need to guess.
As we mentioned above, many regular Sudoku techniques can be used to help solve Calcudoku. But you have some extra clues, so it’s worth using them.
We’ll work through an easy level puzzle to demonstrate common techniques for solving Calcudoku. As with most puzzles, there isn’t a single path from start to finish, so this is not a definitive way to reach a solution, just one possible way.
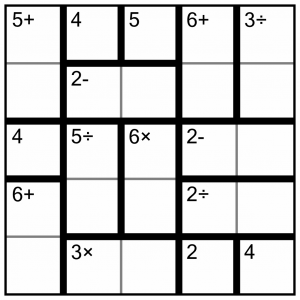
This is the puzzle we are going to solve. It’s an easy level puzzle – partially determined by its size (5x5), but mostly by the simplicity of the calculations, the small size of the blocks, and the number of labelled single cells. That’s where we will begin.
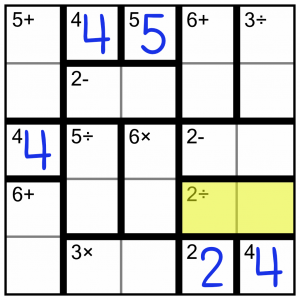
I said this was an easy puzzle! We’ve already filled in five single cells without having to think about it.
Where next? Let’s consider the highlighted block, a two-cell 2÷. We have to divide two numbers to get the answer 2. As this is a 5x5 puzzle, the largest number we can put in is a 5. Therefore the only possible solution to this block is a 4 and a 2 (because 4÷2=2). We have to decide which number goes in which cell, but that’s easy because we’ve already got a 4 and a 2 in the block below. As normal Sudoku rules apply, we cannot have the same number twice in the same column or row, so there’s only one possible way to fill in this block.
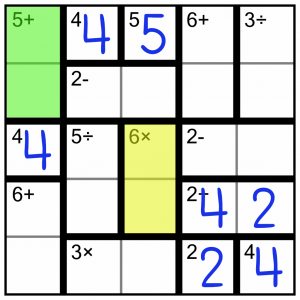
For most of the blocks in this puzzle it’s easy to figure out the numbers we need to fill them, but not necessarily obvious which way around they go within a block. For example, the 5+ block (green), has to contain a 3 and a 2 (it can’t contain a 1 and 4 because the column already has a 4). But which goes in the top cell and which in the bottom? We don’t know yet. We could write the candidates in as little numbers in both cells, and indeed in a harder level puzzle we’d do that. But for an easy puzzle like this, there’s no need. We can just solve other blocks first.
So we’ll look at the yellow 6x block instead. There’s only one possible solution to that. It has to be 2x3, and as we already have a 2 on the grid, we know the 2 has to go in the top cell of this block.
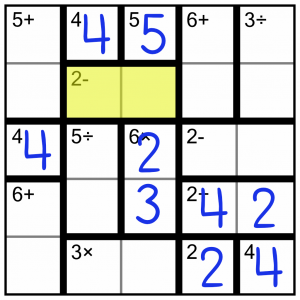
This 2- block only has a single possible solution. It can’t be 5-3 because we cannot put either a 5 or a 3 in the second cell (they’re both already in that column). So it has to be 4-2, and to stay within the rules there’s only one way around we can place those digits.
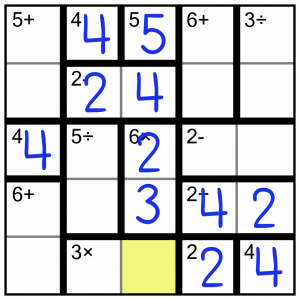
Now we have a no-brainer – a single cell remaining within a column. It has to be a 1, because that’s the only number missing from the column. And filling that in is going to tell us what needs to go with it to complete the 3x block.
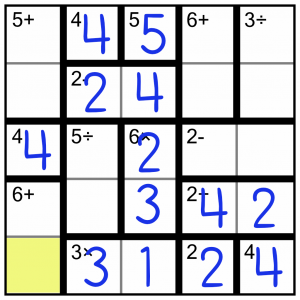
That gives us another easy win cell in the 6+ block (it’s the only missing number in the row), which again tells us how to complete that block.
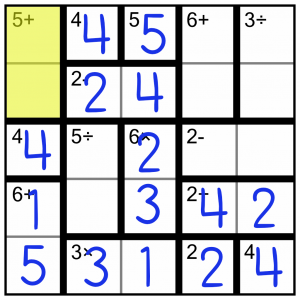
Now we know how to fill in the 5+ block we looked at earlier. We’re missing a 2 and 3 in the column, so it’s 2+3. The 2 in the second column forces the order in which we fill the block.
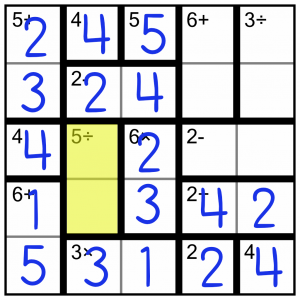
This has to be 5÷1, and the 1 in the first column forces the placement order.
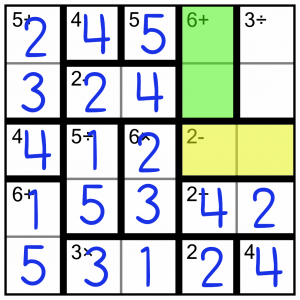
The 2- must be 5-3 (the only valid option). Which way around do they go? Nothing currently on the board tells us. But we can take into account the 6+ (green) block, which has to be 5+1 (it can’t be 3+3 because that would put two 3s in the column, and it can’t be 4+2 because we’ve already got them in that column). Whichever way around we put those numbers in the green block, we’re going to have a 5 in that column, so the 5 in the yellow block must go in the second cell.
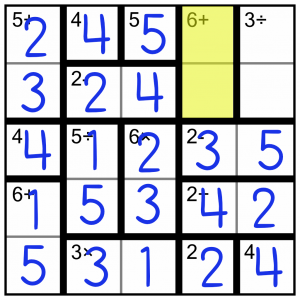
We can fill in the 6+ block because we already know it’s 5+1, and the order is forced by the presence of the 5 in the top row.
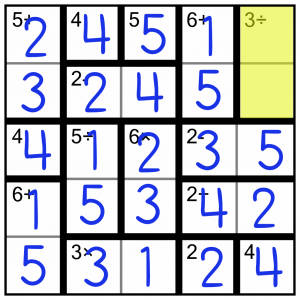
That just leaves this 3÷, which is a no-brainer anyway because it’s made of two single missing cells from the top two rows. We don’t even have to think about the simple calculation (which obviously must be 3÷1)!
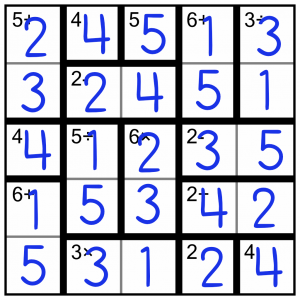
All done. Ready to try some Calcudoku yourself? Read on to find out where you can do just that…
Ready to have a go yourself? We’ve put together a taster of four puzzles for you, including the example above. You can download and print the PDF below. Solutions are included, but no cheating!
Want to try out some Calcudoku? We have you covered. We sometimes include them in our free Puzzle Weekly magazine – you should totally sign up for that if you haven’t already, as it puts 28 brand new puzzles in your inbox every week.
You can also find four levels of Calcudoku puzzles in our Jumbo Adult Puzzle Book – which happens to include more than 500 puzzles of 20 different varieties.