Number Cross

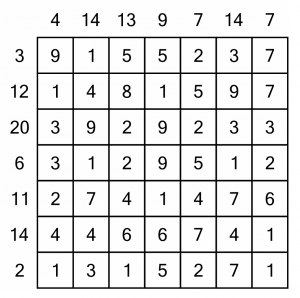
Now you know the theory, we can put it into practice and work through a full size Number Cross puzzle. This is the grid we are going to solve.

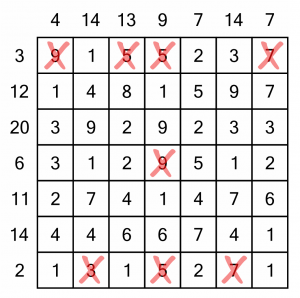
We will begin by going for the easy wins – crossing out any numbers that are larger than the sums for their row or column. That immediately knocks out eight numbers.

Next, we can look to see if there are any numbers that cannot possibly be used in a sum. We’ll do rows first.

In the first row the 1, 2 and of course 3 can all potentially be used to add up to 3, so we have to keep them all.
In the second row, the 9 cannot be used in combination with any of the other numbers to reach 12, so we can eliminate it.
In the third row there are a a few ways of reaching 20. We could add all the 3s together with another 9 and a 2. So all the numbers could potentially form part of the sum.
We keep moving down the rows in that manner, but all the numbers must be kept for now.
Next we can do the same thing but for the columns.

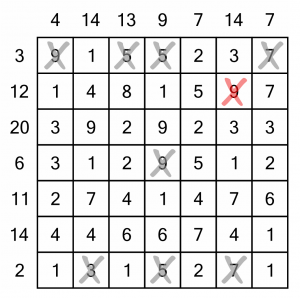
We can’t eliminate anything in the first column. We can lose the 7 in the second one because that can’t be combined with anything to reach 14. The third column draws another blank.

In the middle column, things get interesting! Because of the numbers we already eliminated in the previous step, we can see that the only way to reach 9 is to use the 9 in that column. We can cross out all the other numbers in the column. It can be handy to also circle the 9, because we know we will have to use it in the row adding up to 20. Highlighting it with a circle will make it easy to remember that later. We can also cross out the 9 outside the grid so we know we’ve completed that column.

Continuing across the columns we get to eliminate one more number, the 4 in the fifth column.

We’ve eliminated a fair few numbers already, and completed a column. Glancing at the grid, the sum-11 row merits closer inspection because we’ve crossed out 3 numbers already…

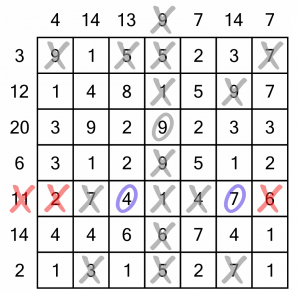
The only way to reach 11 is with the 7 and the 4. We can circle them, cross out the other numbers, and cross out the 11 outside the grid to mark that row complete.
Circling those two numbers may have further consequences that we should investigate. First, the 4. We know we have to use it in the sum-13 column. Does that eliminate any further numbers? Unfortunately not; they could all be combined with the 4 to reach 13. The same is true in the sum-14 column – all the remaining numbers can be combined in some way with the 7 we know we must use.
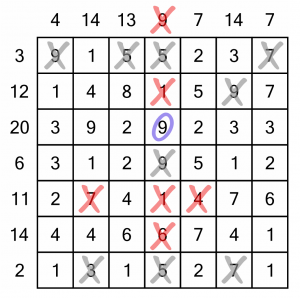
Let’s go back and go through the rows and columns again, but this time instead of just looking for numbers that can't be used in a sum, also see if there are any that must be used regardless of how it’s calculated.

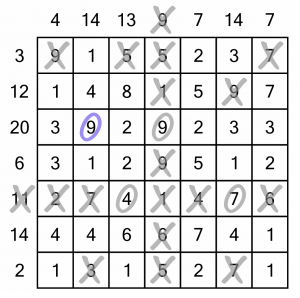
This yields a 9 in the sum-14 column. However we reach the sum of 14, the 9 has to be included – the other numbers aren’t sufficient without it. We can circle it, and then see if that has a consequence for its associated row (the sum-20 row).

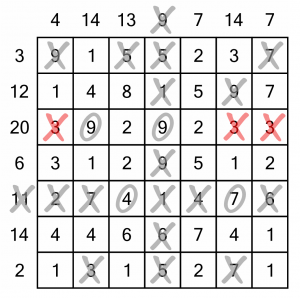
Indeed it does! Now we know that we are using two 9s, we can deduce that we need one of the 2s to reach our target of 20. Therefore we can eliminate the 3s. That means we can look at three columns for knock-on consequences.

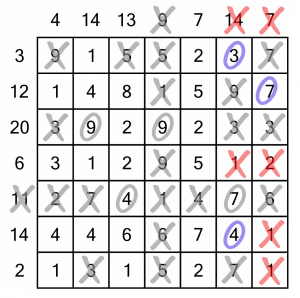
The first of the 3s was in the sum-4 column, but it doesn’t help.
The second 3 was in the sum-14 column. Now it’s gone, the only way to reach 14 (given the 7 we already circled) is with the 3 and 4. We circle them, cross out the remaining 1, and cross off that column as complete.
The final column (the sum-7) can also be completed – it has to be the 7. We’re getting somewhere!
We’ve crossed and circled quite a few numbers, so a quick run through the rows is in order.

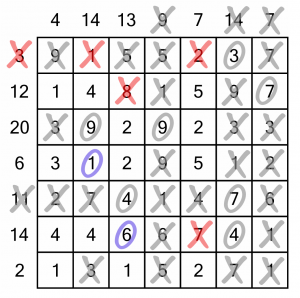
The first row (sum-3) is already complete, so we can cross it off.
We can cross out the 8 in the second row because there’s no way to combine it with the 7 we know we have to use to reach 12.
In the sum-6 row, we know we’ll have to use the 1 regardless of how we reach the goal, so we can circle that.
In the sum-14 row, now we know we have to use a 4, we can eliminate the 7. We also know that we’ll have to use the 6, so we can circle that.
Then we’ll work through the columns again.

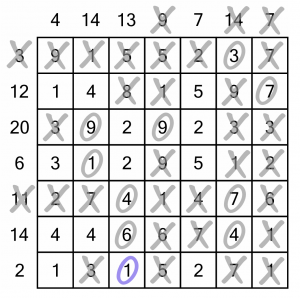
It doesn’t yield much, but we do know we’ll have to use the 1 in the sum 13 column, so we can circle it. That has a consequence for the sum-2 row at the bottom...

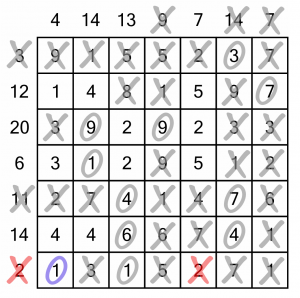
It allows us to complete that row. We’re almost done. Completing the final row has some knock on consequences so we’ll go through the columns again.

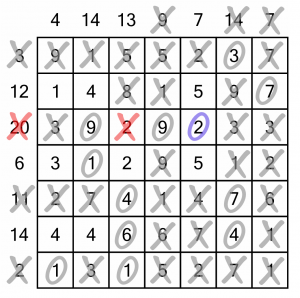
It’s left us with only a single 2 in the sum-7 column, so we know that must be used and can be circled. Doing so completes the sum-20 row, so we can mark that as done and eliminate the remaining 2 in that row.

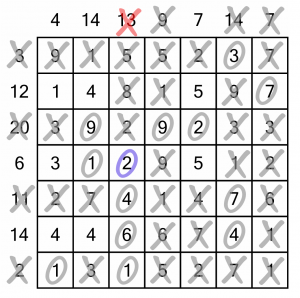
Knocking out that 2 lets us complete the sum-13 column...

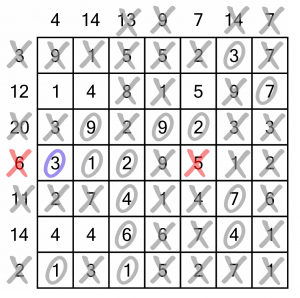
And that in turn allows us to solve the sum-6 row. Now it’s an easy run to the end...

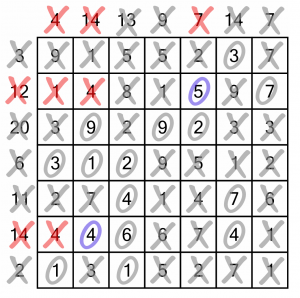
The remaining rows and columns have single solutions.