Meadows is a spatial awareness logic puzzle played on a square grid containing circles.
In a hurry? Jump to: Rules / Tips / Worked Example / Video Tutorial / Download Free Puzzles / Books
Here’s what a small puzzle looks like.
There is just one rule in meadows: split the grid into squares, such that each square contains a single circle. That’s it! Sounds easy, right? Small puzzles certainly are. But don't be fooled, they can get tough very quickly. Here’s what our small sample puzzle looks like once it’s been solved.
These puzzles are solved by using spatial constraints and logical deduction. Here are some tips to help you get started, then we’ll work through an example puzzle to put them into practice.
The best way to understand the puzzle is to work through one. Our puzzles have only one valid solution, but there are almost always a number of ways of arriving at that solution. This example is not intended to show the best or most efficient way to solve the puzzle, but to demonstrate common techniques you can use to do so.
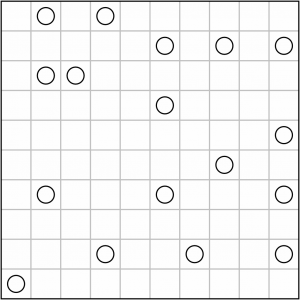
This is the puzzle we are going to solve. It’s a level 1 puzzle, so pretty easy. It doesn’t require complex chains of logic to reach the solution.
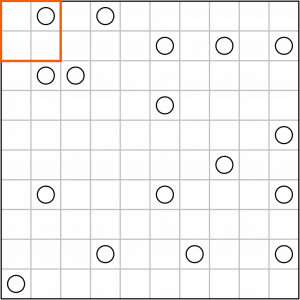
We’ll start in the top-left corner. This boundary has to form the top and left edges of a square, we just need to find the bottom and right ones. The smallest possible square we could draw, taking in a circle, would be 2x2. And indeed that’s also the largest we can draw, because if we tried to go up one size to 3x3, we’d be including two more circles. So we have to draw in a 2x2 square here, there’s no other option.
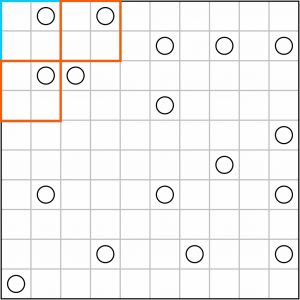
We can work outwards from this corner and put in a couple more 2x2 squares. These are, like the first, constrained in that they cannot be any smaller or they wouldn’t contain any circles, or any bigger because then they’d contain too many.
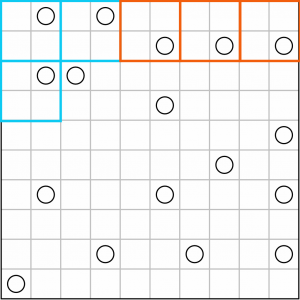
Working along the top, we can put three more 2x2 squares in. These are all constrained in the exact same way as the other squares we’ve drawn so far.
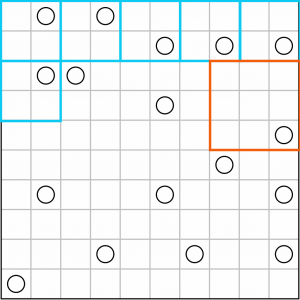
We can carry on going clockwise around the puzzle and work our way down. The next square has to be at least three cells tall to reach the next circle. We can’t go further than those three cells or we’d be including a second circle. So this has to be a 3x3 square. If we tried to make a smaller square around that circle, we would be orphaning the empty cells above it.
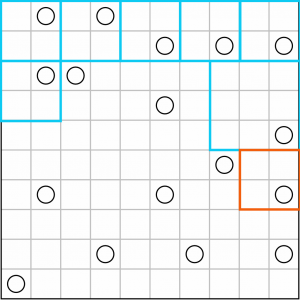
Continuing down this edge, the next square is constrained by the circle to its left. It has to be 2x2.
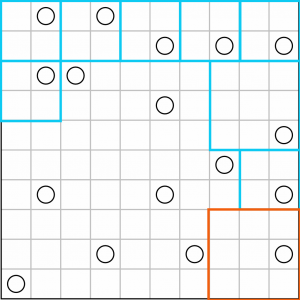
That shows that we have to put in a 3x3 square in the bottom corner as the only possible way to take in that bottom right-hand circle without grabbing any others and without leaving empty space.
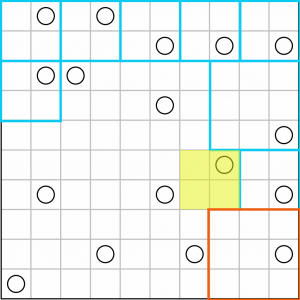
That last square has given us half a square here – we just have to draw in the other half.
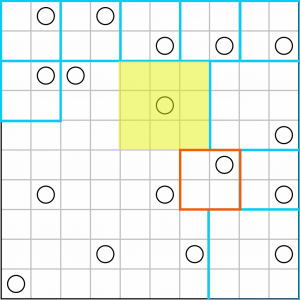
Drawing that in means we now have three boundaries for this area. There has to be a square here.
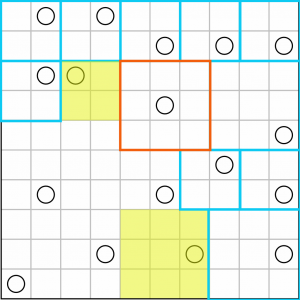
We have two more partially created squares here…
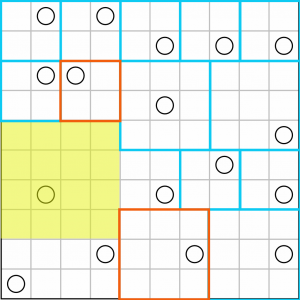
…and drawing those in suggests a big 4x4 square here. It has to be this big, because there’s no other way to include all that empty space in any other square along with a circle.
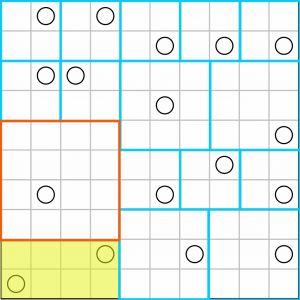
That just leaves these eight cells, which we only need to cut in half to make two squares…
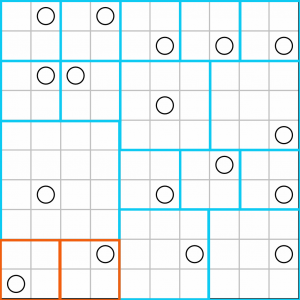
…like this.
And that’s it, we’re all done! Every square has a circle, every circle is in a square. Puzzle solved.
How did you get on? Did you race ahead and solve it before the end of the explanation? Are you ready to try some yourself? Read on for more.
We’ve put together a taster of four puzzles for you to try out, including the example above. You can download and print the PDF below. Solutions are included, just in case you get stuck.
Want some more Meadows puzzles? We've got your back! Puzzle Weekly Presents: Meadows is a collection of 120 brand new puzzles. Set over seven levels of difficulty, it's perfect for players of any level.
We also publish Meadows puzzles in Puzzle Weekly from time to time. Puzzle Weekly is our free weekly puzzle magazine – find out more, and get your copy, here