Kakuro is an addition based puzzle played on a grid a bit like a crossword. The objective is to fill the grid such that the numbers add up to the clues shown. Here’s what a small puzzle looks like:
The rules of Kakuro are as follows:
Here’s what the sample puzzle above looks like when it’s been completed:
Solving these puzzles is all about working with known information to narrow down possible digit placements until you can determine definite positions. There’s a single valid solution for any given puzzle, and no need to guess – logical deduction can get you to the end. However, as puzzles increase in difficulty, there may be extended chains of logic required to reach a solution.
Here are some tips to help you, and then we’ll work through a puzzle to put some of them into action.
Let’s put some of those tips into practice by working through a puzzle from start to finish. Although our puzzles have single valid solutions, there are usually lots of different ways of reaching it. This example is not intended to show the best or fastest way of solving the puzzle, just one possible way.
This is the puzzle we are going to solve. It’s a Level 1 puzzle – pretty small, with some pre-filled numbers – and does not require extended chains of logic to solve.
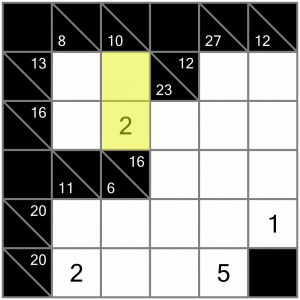
There are a couple of places we could start, given the pre-filled cells. Let’s begin near the top. This vertical sum needs to add up to 10, and we’ve already got the 2, so this is an easy win – we can enter the 8 to complete the sum.
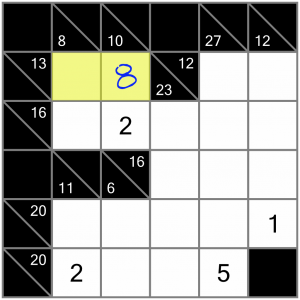
Having filled in the 8, we now have another simple sum. We’re looking for 13 to complete this horizontal sum, so we can fill in a 5.
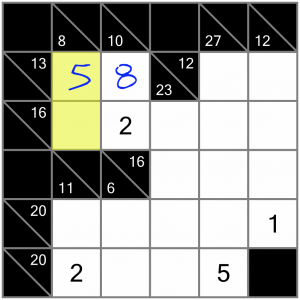
That in turn lets us complete this vertical sum. We need it to add up to 8, so we can put in a 3 and we’ll have finished that corner of the puzzle.
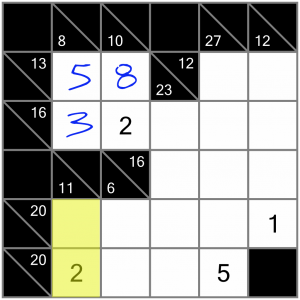
There’s another easy win down in this corner.
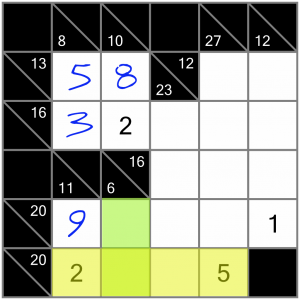
Now let’s have a look at this horizontal 20 sum. We’ve already got it half filled, so maybe there aren’t too many options left to complete it. A quick look at the Killer Sudoku calculator shows the following number combinations that could be used, bearing in mind we already have a 2 and a 5: 2+4+5+9 and 2+5+6+7.
Of those, we can eliminate the second. Why? Because of the vertically crossing 6 sum, highlighted here in green. Putting either 6 or 7 in the cell where the two sums intersect would not allow us to complete the 6 sum correctly. Therefore the numbers we need to complete the 20 sum must be a 4 and a 9. And by the same reasoning, we cannot put the 9 in that intersecting cell, so it has to be the 4. We have all the information we need to complete this horizontal 20 sum.
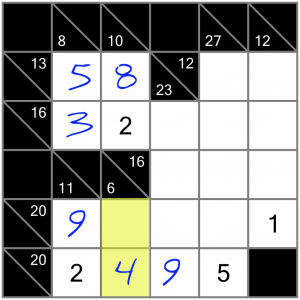
Now we know how to complete this vertical 6 sum.
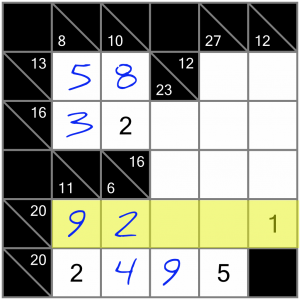
This 20 sum is only missing two digits, so seems to be worthy of closer examination. If we check the Killer Sudoku calculator again (or use the Cheat Sheet), we discover there’s only one set of numbers that can complete the sum and incorporate the 9, 2 and 1 that are already in place: 1+2+3+5+9. So we’re missing a 3 and a 5…
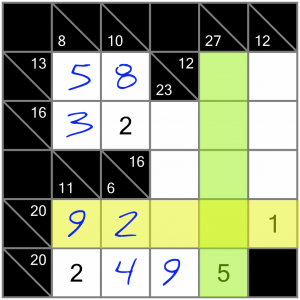
…and the 5 in this crossing sum means that we cannot put the 5 in the intersecting cell (or we’d have two 5s in the same vertical sum, which is not allowed). So there’s only one way to complete the 20 sum correctly.
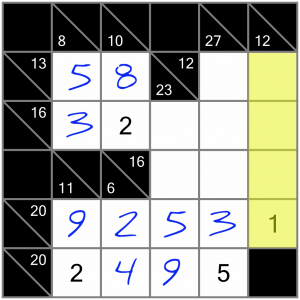
Now let’s have a look at this vertical 12 sum. There’s a reason I’ve skipped over to this side of the puzzle. A four-cell 12 sum is of interest because it contains two required digits. Which is to say however you complete it, it has to contain a 1 and a 2 because either it’s 1+2+3+6 or it’s 1+2+4+5.
We’ve already got a 1 in there, so we know one of the other cells has to contain a 2. Of the three empty cells, one of them can’t contain a 2 because there’s already one in the horizontal 16 sum that crosses it. So we can write small candidate 2s into the other two cells. These might help us later.
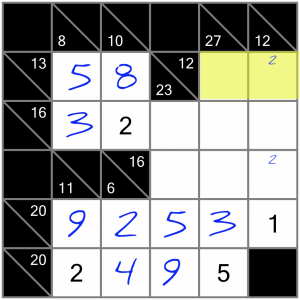
What options do we have for this horizontal 12? It could be any of the following:
3+9, or 4+8, or 5+7 (it cannot be 6+6 because digits cannot be repeated in a sum). Notice anything about these three sums? None of them contain a 2. Therefore that little 2 candidate number we filled in here cannot stay…
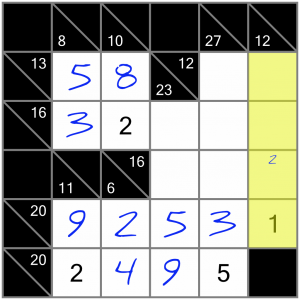
…which leaves just one possible place to put the 2 in this sum.
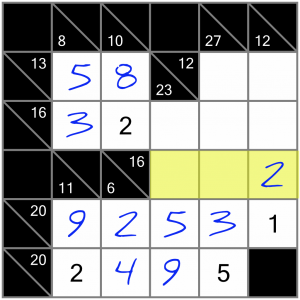
Now let’s turn our attention to this horizontal 16 sum. We’ve only got two cells to fill, so we’ll have a look at the trusty calculator again, to see what combinations of numbers include the 2 we’ve already got. Our options are 2+5+9 or 2+6+8. Can you work out which of this is correct?
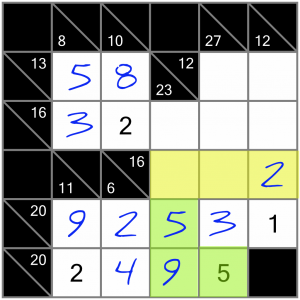
These two 5s and the 9 mean there’s no way to fit a 5 and a 9 into our yellow cells together. So the answer must be that these cells are filled with a 6 and an 8. We don’t yet know which goes into which cell, so we’ll just write them in as small candidate numbers for now.
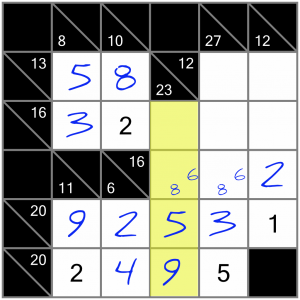
Those candidate numbers might help us with this vertical 23 sum. We can look for combinations of numbers that include the 5 and 9 we’ve already got, and then narrow those combinations down further to only those that also contain either a 6 or an 8, since we know we have to have one of those digits in this sum. These are our options: 1+5+8+9 or 3+5+6+9. That means our top cell in this sum contains either a 1 or a 3…
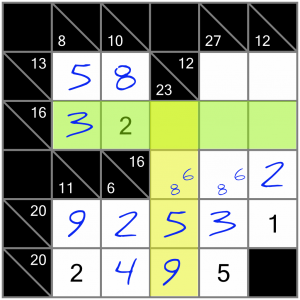
…and since there’s already a 3 in the crossing 16 sum, we can’t put another one here. So the top cell has to be a 1…
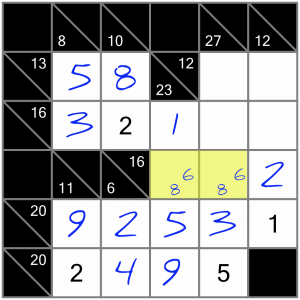
…which means we can now solve these two cells (since the one on the left has to be an 8, to complete the 23 sum).
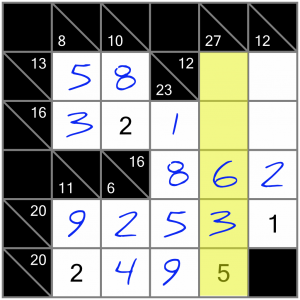
There are a few places left to fill. We’ll look at this 27 sum next. Given we already have a 3, a 5 and a 6, the only combination of numbers that works for this sum is 3+4+5+6+9. So our two empty cells contain a 4 and a 9. to work out which goes into which, we can again turn to the sum that crosses this one.
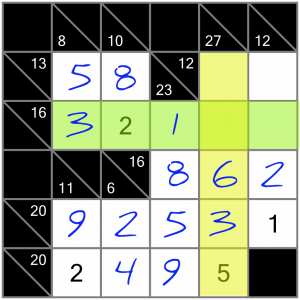
If we put the 9 into the intersecting cell, the horizontal 16 sum would add up to 15 with one cell remaining. That would mean we’d have to put a 1 in the last cell of that sum, but that sum already has a 1, so we cannot do that. Therefore we must put the 4 into the intersecting cell, leaving the 9 to go in the top cell…
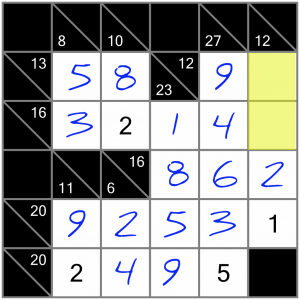
…like this.
That leaves just two cells to fill, and since each one is a single missing cell for a horizontal sum, they are easy fills.
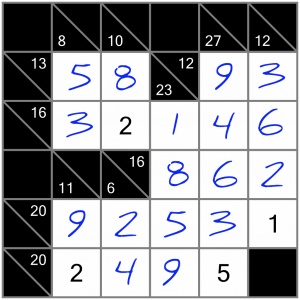
There, that’s it - all done. How did you get on? Did you rush ahead and finish the puzzle before reading through this example? Are you ready to try some more? Read on!
We’ve put together a taster of four puzzles for you, including the example above. You can download and print the PDF below. Solutions are included, but no cheating!
Ready for more Kakuro? As luck would have it, we can help! You'll find 120 puzzles spread over seven levels of difficultly in Puzzle Weekly Presents: Kakuro. With one puzzle per page, there's plenty of room for notes and candidates.
We all include seven levels of Kakuro puzzles in Puzzle Weekly from time to time. Puzzle Weekly is our free weekly magazine – find out more, and get your copy, here.