Bricks is a Suduko-like puzzle played on a square grid. The aim is to fill the grid with numbers.
In a hurry? Jump to: Rules / Tips / Worked Example / Video Tutorial / Download Free Puzzles / Books
Here’s what a small Bricks puzzle looks like:
The rules of Bricks are as follows:
Here’s what the earlier example puzzle looks like when solved:
Bricks puzzles are solved through a process of logical deduction. By narrowing down placement possibilities for each digit, you can gradually fill in the grid. Here are some tips to help you get started. In a moment, we’ll work through an example puzzle to see the theory in action.
All our puzzles have a unique solution, but there are lots of ways to reach it. This example is not intended to show the best way, or even the most optimal way to solve the puzzle. It is simply a way of showing some of the techniques you can use do to so.
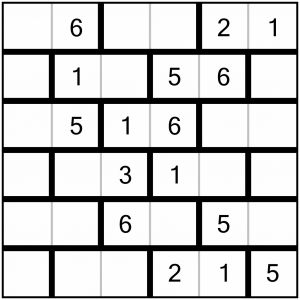
This is the puzzle we will be working on. It’s a Level 1 puzzle – small, and, with almost half the numbers already filled in, easy. There are no complex chains of logic necessary to solve it.
Being a 6x6 grid, we are looking to fill each row and column with the numbers 1 through to 6.
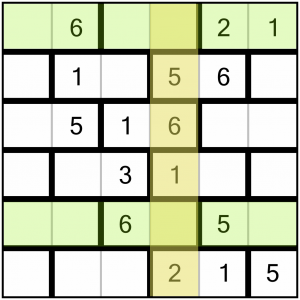
Although it’s an easy puzzle, there are no rows or columns with only one digit missing, so we’re going to have a look a little bit harder to find where to start.
This column is only missing a 3 and a 4. Neither row that crosses it contain a 3 or a 4, so we cannot use the rows to determine which empty cell contains which number. But we can use the fact that every brick must contain an odd and even number.
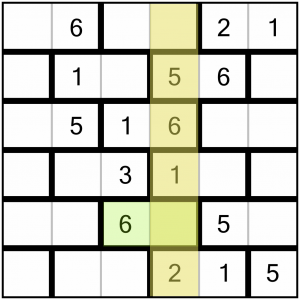
This brick contains a 6, so it cannot also contain a 4 because that breaks the rule. Therefore this empty cell must contain the 3, leaving the first cell in the column to take the 4.
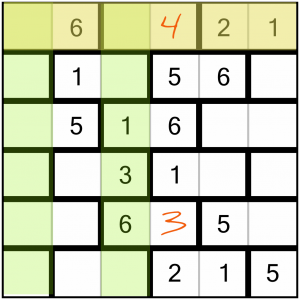
This top row now only has two empty cells remaining (a consequence of filling in that 4). As such, it’s probably easy to complete. It’s missing a 3 and a 5. Checking the two columns that cross the empty cells, we can see that one of them has a 3 in it already, so must take the 5. That leaves the 3 to go in the top left.
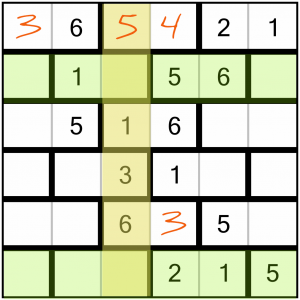
The 3 in the top-left corner doesn’t help get us any further. The 5 we just filled in is more useful though. Now we have this column with only two empty cells, and we need to fill them with a 2 and a 4. There’s a 2 already in the crossing row at the bottom, so that tells us how to complete this column.
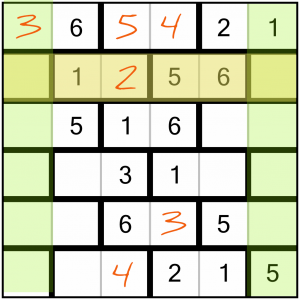
The knock-on effect of filling in the 2 in that column is that this row is now only missing a 3 and a 4. The 3 in the first crossing column tells us that the first cell cannot contain a 3 (because that would be two 3s in the same column, which is not allowed). So the 4 goes in the first cell and the 3 in the last one.
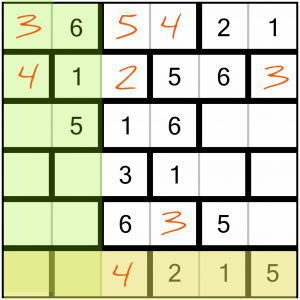
Here’s another row with only two missing numbers. We need to find homes for the 3 and the 6. That 3 in the top-right corner again tells us which goes where. Turns out filling in that 3 earlier on was quite useful after all.
Note that we could also have solved row by looking at the brick containing the 4. It could not take the 6 because that would put two even numbers in the same brick, which isn't allowed. As I said, there are lots of ways of reaching the solution!
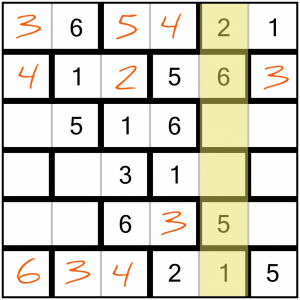
Here’s a column missing a 3 and a 4. Can you see where they go? It’s pretty easy to work out, there are two different means of determining which number goes where.
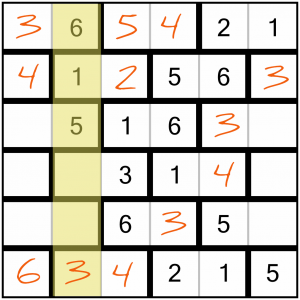
Filling in that last 4 makes it possible to complete this column now. It needs a 2 and a 4, and since we already have a 4 in one of the rows, we know which number goes in which cell.
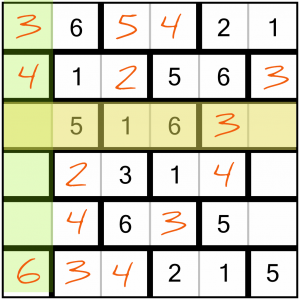
Nearly there now. This row needs a 2 and a 4. The first crossing column already contains a 4, so it will have to go in the last cell, leaving the first one to take the 2.
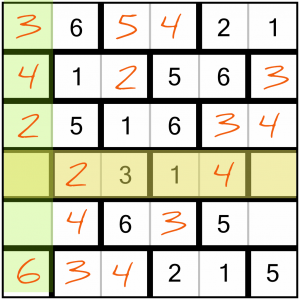
This row needs a 5 and 6. Again, the first crossing column has a 6 already, so that's all the information we need.
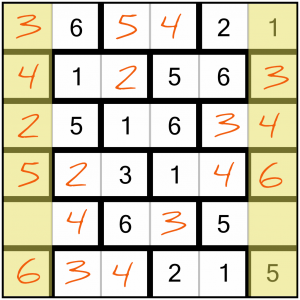
That just leaves these two columns, each of which are missing a single digit – it doesn’t get any easier than that!
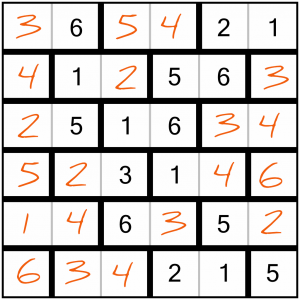
And that’s it, we’re all done. I said it was an easy one! Did you get to the end before finishing this example? Ready to try something a little harder? Read on…
We’ve put together a taster of four puzzles for you, including the example above. You can download and print the PDF below. Solutions are included in case you get stuck, but no cheating!
Want to try your hand at Bricks? We have options! There's Puzzle Weekly Presents: Bricks, which includes 120 puzzles (one per page) over seven levels of difficulty. It's amazing value.
We also include seven levels of Bricks puzzles in Puzzle Weekly from time to time. Puzzle Weekly is our free weekly magazine – find out more, and get your copy, here.