Creek is a spatial awareness puzzle played on a square grid. The aim is to fill certain cells, leaving a clear path – the creek – that can be traversed without blockages.
In a hurry? Jump to: Rules / Tips / Worked Example / Video Tutorial / Download Free Puzzles / Books
Here is an example of a small Creek puzzle.
The rules of Creek are very simple:
Here’s what our example puzzle looks like once it’s been solved.
Solving these puzzles requires a combination of elimination, forced placement, and logical deduction. Here are some tips to help you get started, then we’ll work through a puzzle from beginning to end.
We will work through a sample puzzle from beginning to end. Although our puzzles have a single valid solution, there’s no single path to reach it. This is just one way to get to the end of this puzzle, and may not be the most efficient as the aim is to demonstrate different solving techniques.
This is the puzzle we are going to solve. It’s a level 1 puzzle, so it’s quick and easy to complete, without requiring lengthy chains of logical deduction that may be necessary in harder puzzles.

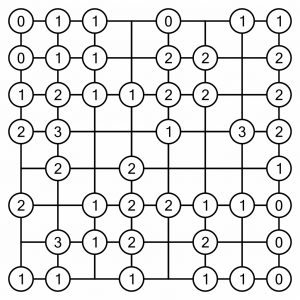
We’ll begin in the top right, because that’s the easiest of easy wins. The 1 in the circle only touches one cell, so we know we have to fill it. We can cross out the 1 in the circle, as we have met its target. We can also cross off the other 1 touching this cell, because we’ve met its target too. Two for the price of one!
I like to put a mark in cells that I know cannot be filled, because it makes it easier to see which ones to fill later. So I’ve put a dot in the cell touching that second 1 at the top right – we know it can’t be filled.
Working down the right hand side of the grid (as I’m going clockwise), the 2s are all easy fills because they each touch two cells. That also allows us to cross out the 1 on that edge.
We can cross out the 0s because nothing touching those can be filled, and for the same reason we can add dots to the cells that touch them.
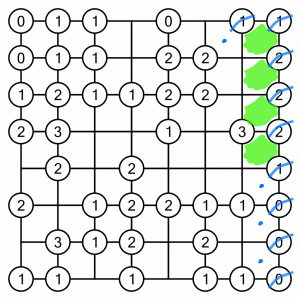
Continuing clockwise, along the bottom row we can fill in a couple of cells, which lets us strike off four 1s as complete, and also mark another couple of cells as having to remain empty.
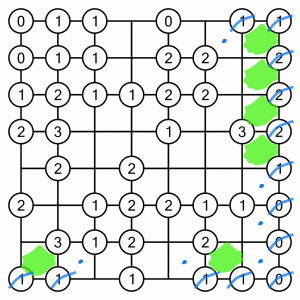
Now working up the left-hand side, the two 2s are easy fills – we have to fill both cells touching them in each case. Filling those cells also lets us cross of a 2 one column further in, and it also lets us cross of a 1 on the edge.
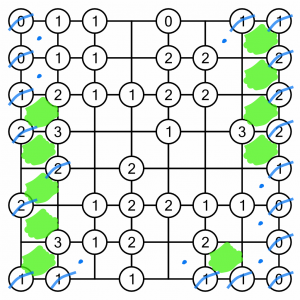
The top two cells both touch 0s so can be marked as empty. For completeness, I’ve struck out the 0s to make it easier to see where we are up to.
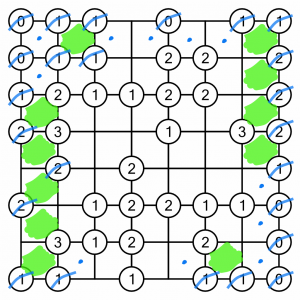
There’s only one cell to fill in on the top row, but doing so lets us cross of four 1s. The other cells must all be blank, so we can put dots in them.
We’ve completed a circuit of the grid. Now we can keep working inwards, like peeling an onion.
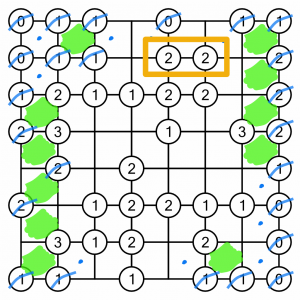
In a bigger puzzle, it usually makes sense to work methodically inwards one cell at a time. This is a small puzzle though, so we can work our way around doing several easy fills at once. Take these 2s for example. They are easy to fill because we’ve eliminated the cells above them, meaning we have to fill those below…
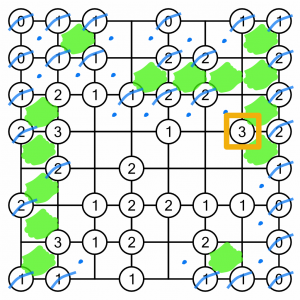
…like this. That let us cross out four 2s and a 1, and eliminate a several cells as well.
If we keep working clockwise, we can see that this 3 needs another cell to be filled, and there’s only one candidate remaining, so we have to fill that.
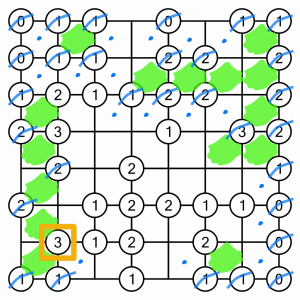
We could keep going down and fill out some more cells using logical deduction, but why use up the brainpower when there are still easy wins on the board? This 3 is another simple one – there’s only one cell we can fill in to complete it.
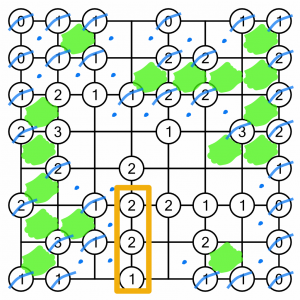
Completing that 3 let us strike off a couple of 1s, which allowed us to eliminate any other cells touching those 1s, which means it’s now very easy to complete these three circles.
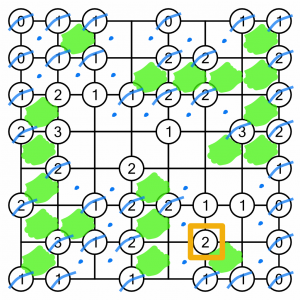
That’s eliminated more cells, so we can complete this 2, which is also going to complete the 1s above it.
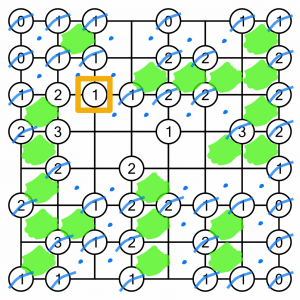
Only a few circles left to knock out now. This one is a no-brainer, it only has one valid cell touching it. Completing it will also complete the 2 to its left and the 3 below that.
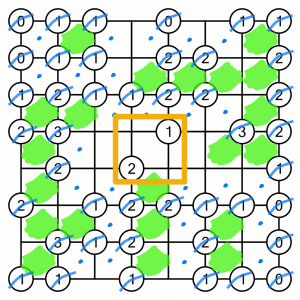
That just leaves this 1 and 2. At first glance, it looks like there are two ways we could complete this. We could fill the cell to the bottom right of the 1, and the cell to the top left of the 2. This would meet the criteria for the circles, but it would cut the unfilled cell creek into three distinct parts…
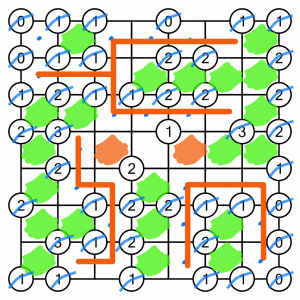
…like this. I’ve added the red line to make it easier to see the path of the creek. The rules state it must be continuous, which is not the case. So the solution must be something else.
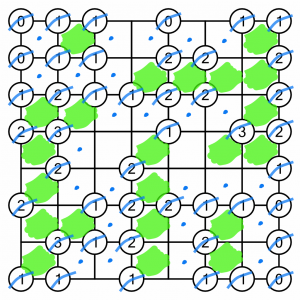
In fact we only need to fill one cell to complete both the 2 and the 1, and that leaves a continuous creek.
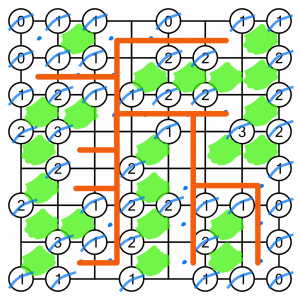
Here’s the creek highlighted with the red line again. All the empty cells can be reached by travelling horizontally and vertically, and all the number targets have been met, so the puzzle is complete.
How did you get on? Did you get ahead of me and solve the puzzle before the end of the tutorial? Ready to try some more? Read on!
We’ve put together a taster of four puzzles for you to try out, including the example above. You can download and print the PDF below. Solutions are included, just in case you get stuck.
Want to try your hand at Creek? We have options! There's Puzzle Weekly Presents: Creek, which includes 120 puzzles (one per page) over seven levels of difficulty. It's amazing value.
We sometimes also include Creek in our free Puzzle Weekly magazine – you should totally sign up for that if you haven’t already, because who doesn’t want at least 28 free puzzles every week?