Trilogy is a pure logic puzzle that uses symbols on a square grid. The aim is to fill the empty cells on the grid with the correct missing symbols.
In a hurry? Jump to: Rules / Solving / Tips / Worked Example / Download Free Puzzles / Trilogy Books
Here’s what a small Trilogy puzzle looks like:
There are three symbols used in the puzzle: circles, squares, and triangles. There are only two rules to remember:
Here’s what the earlier example looks like once solved:
Solving these puzzles requires the application of logic. There are lots of patterns you can use to help you, and the more puzzles you do, the more easily you’ll spot the patterns.
These patterns are all “forced moves” – they allow you to immediately place a new symbol on the grid. Easier puzzles have more of these patterns, but they’ll help with harder puzzles too; as you add more symbols, more patterns will emerge.
In this tutorial we will use the notation A, B, C, and x, where A, B and C stand in for the three symbols and x is the cell we are trying to solve.
There are two kinds of pattern. The easiest is a simple row of four cells with a gap, allowing you to place a symbol:
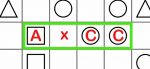
AxCC pattern. In this case, the x must be the same as the A symbol. It can’t be B because otherwise we’d have (ABC)C, which isn’t allowed, and it can’t be C because otherwise we’d have A(CCC), which is also not allowed.
In this example, A is a square and C is a circle, so the empty (x) cell must be a square.
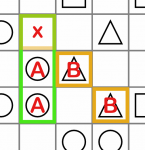
ABxB pattern. In this case the empty cell must contain the A symbol, because (ABC)B isn't allowed, and A(BBB) is not allowed.
In this example, A is a square and B is a triangle, so the empty (x) cell must be a square.

These patterns are easy to spot as you can quickly look for doubles on the grid (two symbols the same next to each other), and doubles with a gap between and another symbol next to them.
Next, you can look for intersection patterns. These are patterns where the empty cell we are trying to solve is at the intersection of two patterns. The simplest intersections are a confluence of doubles. For example, if you have AAx in one direction, and BBx in another, x must obviously be C, otherwise we’d be making a triple, which isn’t allowed.
In this example, we have two circles together vertically, forming an AAx, intersecting with two triangles together diagonally, forming a BBx. The intersecting cell (x) must be a C to avoid three in a row. Therefore, in this case it would be a square.
There are lots of these patterns to find in Trilogy. The following table lists some common intersections and what they resolve to. It should be fairly easy to work out why the answer is what it is in each case.
| Solves To: | ||
| AAx | BBx | C |
| AAx | ABx | B |
| ACx | BAx | A |
| AxA | ABx | B |
| AxC | ABx | A |
These are not necessarily all the possible patterns – they are the most common, and a good starting place. As you get deeper into this fascinating puzzle, you will find more that you can add to your arsenal.
Here are some further tips to help you solve Trilogy:
Let’s put all of that into practice and solve a simple puzzle. This is not intended to show the most efficient way of solving this puzzle. The purpose of the example is to demonstrate the strategies we can use to solve Trilogy, and is just one way of getting to the solution.
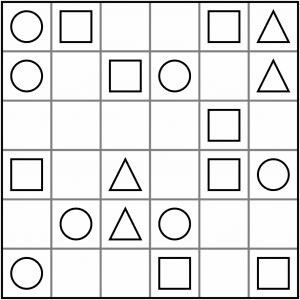
This is the puzzle we are going to solve. We’ve deliberately chosen a simple one to keep this tutorial manageable. The same concepts apply whatever the size of the grid, though.
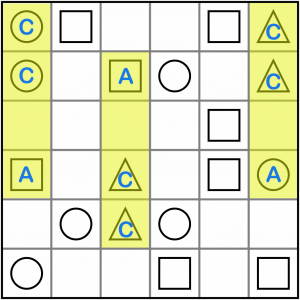
Let’s begin by looking for the easiest patterns. The first of those is the AxCC. There are three of those in this puzzle, all in the vertical plane. We know that the empty cell in this pattern must be the A symbol. If we put a C in there, we’d have three Cs in a row, which isn’t allowed. And if we put a B in there, we would have A, B and C in a row, which also isn’t allowed. So from the left, the first empty cell must be a square, the second also a square, and the third one, on the right edge, must be a circle.
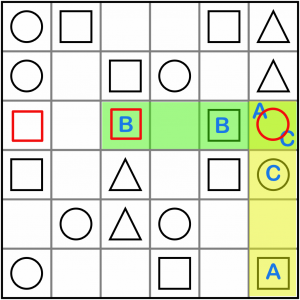
Filling in those three symbols has created a a new AxCC pattern (in yellow), so we know the empty cell must be a square. It’s also given us an ABxB pattern (green). This must solve to A, for exactly the same reason as before. So the empty box in the green area must be a circle.
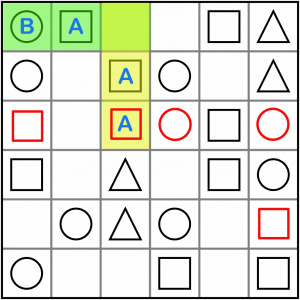
We’ve exhausted the simple gap patterns for now. Let’s look for intersections. The easiest to spot are the doubles (it’s quick to find two symbols the same on the grid). Here’s one example, right at the top. We have an AAx intersecting with a BAx. We know this must solve to B, because if we tried to put an A in the intersecting cell we’d have AAA which isn’t allowed, and if we tried to put a C in there, we’d have BAC which is also not allowed. So the empty cell must contain a circle.
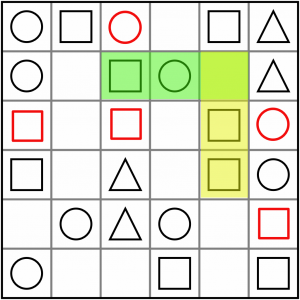
Here’s another, almost the same. This time it’s ABx / AAx, but it solves to the same solution for the same reason. We have to put a circle in the intersecting cell.
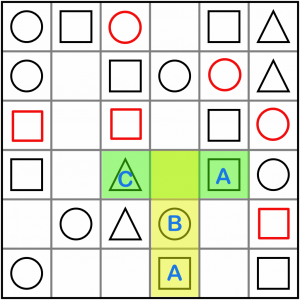
Here’s a different kind of intersection. This is an AxC / ABx. From our table above, we know it resolves to A. That’s because if we tried to put a B in the intersecting cell, we would be creating an ABC run in the green area, and if we put a C in there, we’d be creating an ABC run in the yellow one. A is the only option. The empty cell contains a square.
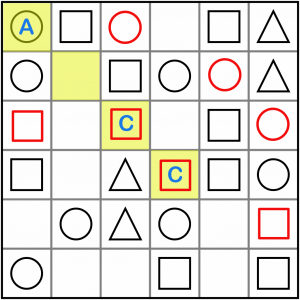
This is an easy puzzle, and there are lots of intersections and patterns appearing all over the place. Let’s look at this AxCC for no other reason than because it’s a diagonal, and we haven’t done any of those yet! It’s important to remember to check the diagonals, particularly when puzzles get harder, as they add two extra dimensions and can often be the key to unlocking the grid.
Being an AxCC pattern, we know the empty cell solves to A, so it’s a circle.
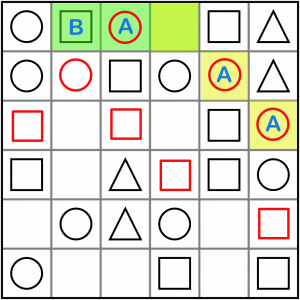
We can do intersections on diagonals as well. Here’s another AAx / BAx, with the AAx on the diagonal. We know it solves to B, so the empty cell at the intersection must be a square.
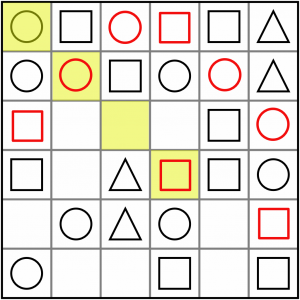
Here’s another diagonal, an AxCC. It must be a square.
And here’s an ABxB. As we fill out the cells, the simple patterns keep popping up again, so it’s worth keeping an eye out for them. This must be a circle.
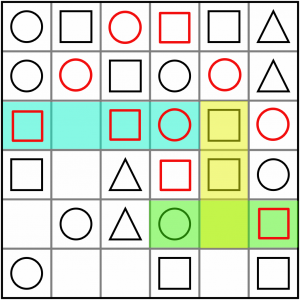
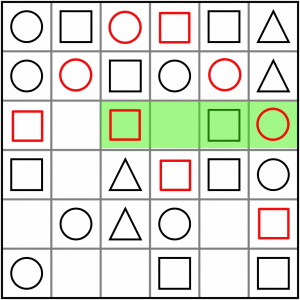
Let’s speed up a bit. We’ve got two patterns here. The blue is another ABxB, so that’s a circle. The yellow and green intersection is an AAx / AxC, so that has to solves to C - a circle in this case.
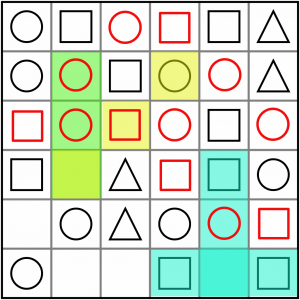
Nearly there. Here are two more. The yellow and green intersection is an AAx / ABx, so must solve to B. It’s a square.
The blue intersection is an AxA / ABx. It must solve to B, so it’s a circle.
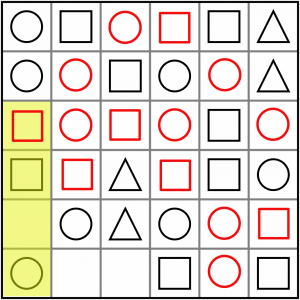
A quick AxCC here. It must be a circle.
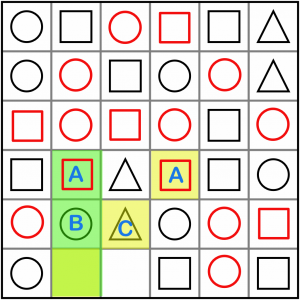
Just two more to go. This is a new intersection: ABx / ACx. This must solve to A (square). If we put a B in here, we’d be creating an ACB run on the diagonal. if we a C in there, it would be an ABC on the vertical. So, it’s a square.
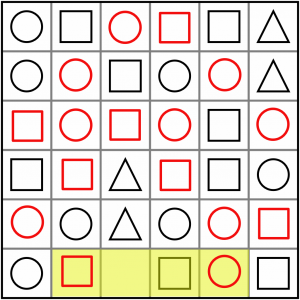
That just leaves us with a simple ABxB pattern along the bottom. It must be another circle.
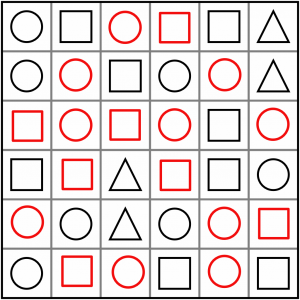
That’s it, we’ve completed the puzzle. And we didn’t even have to draw any triangles! I said it was an easy one. If you want to try some puzzles like this yourself, read on – there are some freebies to download below…
This was a very simple puzzle, but it shows the basic techniques used in solving Trilogy. Harder puzzles have far fewer starting symbols on the board, and fewer (if any) initial patterns. They require using more advanced logic, and notes in the cells as you eliminate possibilities.
Are you hooked? Ready to have a go at some Trilogy puzzles yourself? We’ve put together a sample pack of four grids for you – a couple of easy ones like the above example, and a couple that are more challenging. Download the PDF below. Solutions are included so you can check your results.
Click Here To Download The Taster PDF
Would you like even more Trilogy? We’ve got you covered!
Puzzle Weekly Presents: Trilogy is a collection of 120 puzzles set over seven levels of difficulty. Grab a copy here.
Got a Kobo? We’ve got Trilogy puzzles for that too! Trilogy for Stylus Devices presents 100 puzzles over five levels, and is designed especially for Kobos with stylus. Find out more here.