Sudoku is great fun whatever your age. But when it comes to younger people, this classic logic puzzle can be a fantastic educational tool. Like all the best learning tools, sudoku works well precisely because it is so much fun to play. Kids learn best when they are enjoying themselves, and sudoku has a lot to teach — and not just about numbers. Indeed sudoku, whilst traditionally using numbers, is not a math game. But it has a whole lot to teach.
At the bottom of this page you will find some free sudoku puzzles designed specifically for kids, that you can download and print out. But first, here are seven incredible benefits of using Sudoku as a learning tool.
Right from an early age, very simple kids sudoku puzzles are an excellent way to promote and reinforce the recognition of number forms. Even the simplest 4x4 puzzles are great at this.
By turning recognition into a game, the child is not only gently encouraged to differentiate between figures, but because they must find missing numbers, they will naturally create figures in their mind’s eye. This mental creation of numbers strongly reinforces the forms.
Of course, sudoku doesn’t just have to be played with numbers. Letters can be used instead, adding more learning opportunities. We’ve included both number and letter variants in our free downloadable kids sudoku puzzles at the bottom of the page.
The aim of sudoku is to work out the missing numbers in a grid. The whole game is a puzzle that is crying out to be solved, so naturally playing it encourages and develops problem solving skills.
This can be done as gradually as necessary. A simple grid with a single missing number might seem to be so easy as to be pointless, but it’s like a gateway drug. When a child works out the missing figure, they experience a rush of excitement at having solved the problem; they are primed to solve more.
Building up the difficulty slowly and steadily maintains the challenge. The child is obliged to add a little more effort every time, and think up new ways of finding the answer — and being rewarded with the dopamine hit that comes with success.
As puzzles grow in size, complexity, or both, the child will have to find new ways to solve them. Thus what started as an easy game can soon become a fun and rewarding exercise in lateral thinking.
Larger sudoku puzzles (typically full-size 9x9 and above) are a fantastic tool for encouraging working within a group. Puzzles can be split into racks and stacks, or columns, rows, and blocks, and each piece assigned to one or more children.
With a simple grid, the kids may initially solve the puzzle by working individually on their own portion. But ramp up the difficulty even just a little, and before long they will be obliged to co-operate and communicate to ensure their solutions do not ‘collide’ with those of the others in the group.
Take the difficulty up another notch, and the team will be encouraged to work together to come to a solution for the puzzle, pooling their techniques and knowledge.
For larger groups or older kids, try using 16x16 grids, or even better, Samurai Sudoku. The latter is a ‘multi-sudoku’ game with interlocking grids — perfect for splitting up and working on as a team.
In a sudoku grid, a single mistake inevitably leads to disaster. Just one number out of place renders the entire puzzle unsolvable — not that it’s always immediately obvious!
It only takes a few failed solutions for most children to learn that they must check and double-check their answers before writing them in the grid, thus promoting careful attention to detail.
Logic is essential in solving sudoku, but so is memory. As they work through a grid, a child will be constantly putting numbers into very short-term memory, sometimes for just a few seconds at a time.
Sudoku is a great workout for the brain. Just as concentrated exercise can improve overall fitness, so working short-term memory improves overall memorisation and recall skills. Speaking of working out the brain…
Sudoku demands a level of concentration that just isn’t necessary for most other kinds of puzzles. Simple math games, crosswords, word searches and so on, can all be done piecemeal by dipping in and out as and when. But to solve a sudoku grid effectively, it’s necessary to hold a lot of information in short term memory at once.
Losing focus, or lacking concentration, leads to mistakes or quite simply not being able to find a solution. Therefore the child is obliged to put all their attention into the job in hand. Studies show that concentration is like a muscle, and that repeated training leads to long-term improvement.
If you’ve completed a sudoku puzzle then you know the rush of satisfaction that comes with putting that final number in the grid. One of the amazing things about sudoku is the range of difficulty that can be applied to a single concept. A child can learn the basics on a really easy 4x4 grid in a matter of minutes, yet be constantly challenged and stretched by the exact same set of rules right up to mind-bending super difficult 16x16 grids. Every win is an opportunity to boost their confidence and self-esteem, all whilst having lots of fun.
Now you know why sudoku is such a great learning aid, as well as being a fun game, here are some grids that we have prepared especially for children.
We’ve included three grid sizes: 4x4, 6x6, and regular 9x9. There are eight 4x4 puzzles, and twelve of each of the larger sizes (which also include letter-based variants). Full solutions are of course also included.
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.
The pages have been formatted so they will print on both American letter paper, as well as standard A4.
We’ve got you covered! We publish a brand new free puzzle every day. And of course, we have a large range of sudoku puzzle books of varying difficulty and size.
For kids sudoku, we highly recommend Amelia Baker’s range of books, which we collaborated on. You can find out more about those here. Amelia’s books include excellent tutorials written specifically for younger players, and lots of puzzles from 4x4 to 9x9.
If you want to try your hand at suguru but don’t know where to start, you’ve come to the right place. Assuming no prior knowledge of this captivating puzzle, we’re going to look at how the grid works, cover the simple rules, then dive in to the techniques we can use to solve it. Let’s get started, by looking at…
Suguru grids do not have to be square. It’s possible to make puzzles of various shapes and sizes. Here at Puzzle Genius we are purists at heart, and we prefer the perfection of the square form. But we do publish puzzles of differing sizes — and of course — different levels. To start us off, here is an easy 1-star grid, six cells across by six down. It’s taken from our popular Pocket Suguru series:
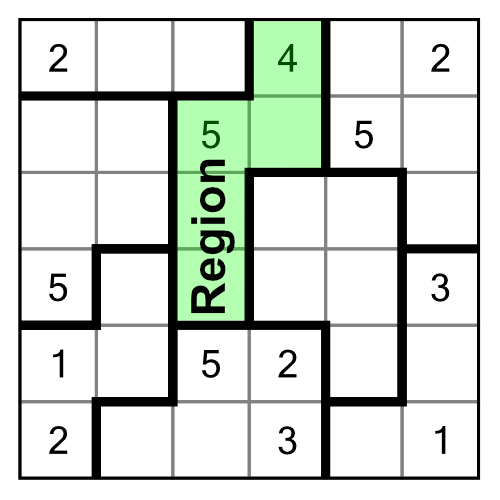
Like a sudoku grid, we have some numbers filled in to start us off (clues). But that’s where the similarity ends. You’ll see there are no columns, rows, or blocks here. Instead we have regions.
There is no fixed number of regions in a suguru grid, and the regions are not of fixed sizes. Indeed those two variables, along with the number of pre-filled clue cells, contribute to the difficulty of the puzzle.
Suguru’s rules are very simple. In fact there are only two:
Looking back at our example grid, we note that the green shaded region has five cells, so it must contain all the digits from 1 to 5.
When we talk about neighbouring cells in suguru, we mean any cell that touches another horizontally, vertically, or diagonally. Here’s our example grid again:
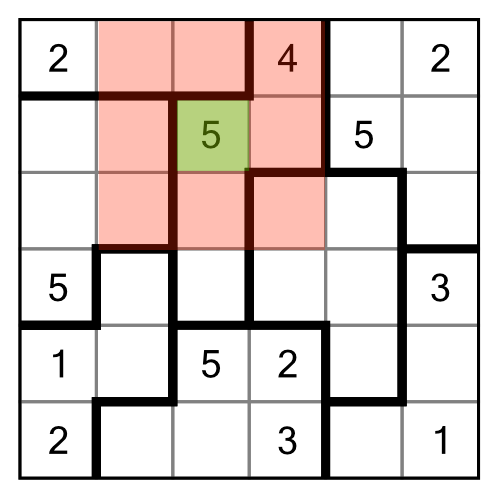
If we consider the green cell 5, all the cells shaded red are its neighbours, so none of them can contain the number 5.
Just as with sudoku, we can always solve a suguru puzzle with logic. Guessing is not a strategy.
Just like sudoku, some cells in a suguru puzzle are very easy to solve right off the bat with nothing more than a simple application of the rules.
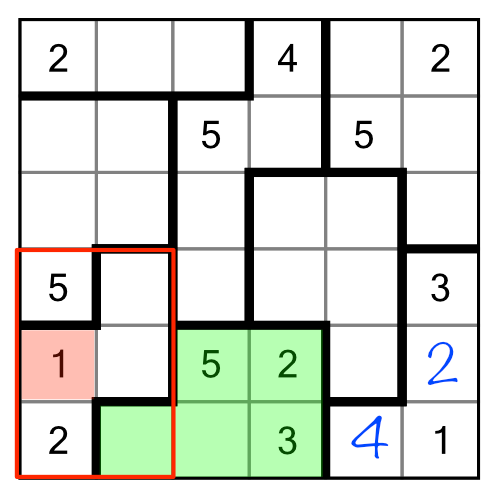
Our puzzle has a an obvious place to begin. The region in the bottom right has four cells and is missing a 2 and a 4:
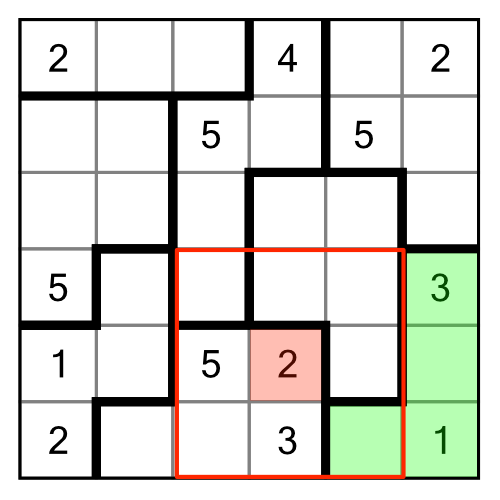
The presence of the 2 highlighted in red means we cannot put another 2 anywhere inside the red outline. That rules out one of our empty cells in the green region. Therefore the 2 has to go in the other one, in turn leaving only one place for the 4.
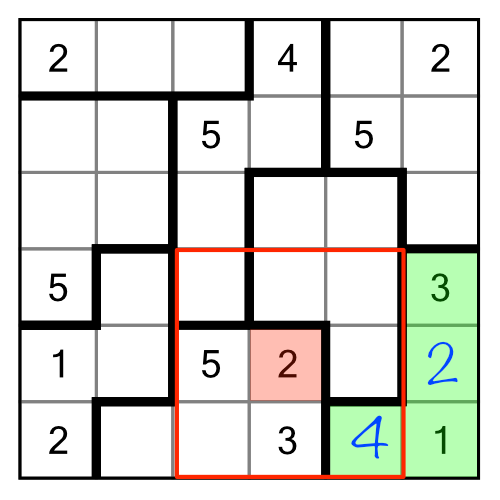
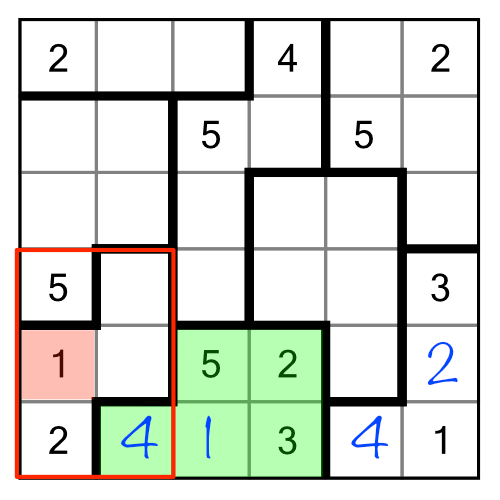
We can apply the same logic here:
Our green region is missing a 1 and a 4. The red highlighted 1 rules out the left-most free cell in our region, leaving only one place it can go. The 4 must therefore go in the other one.
We can quickly fill in another couple of cells the same way:
The red highlighted 4 makes them easy to work out.
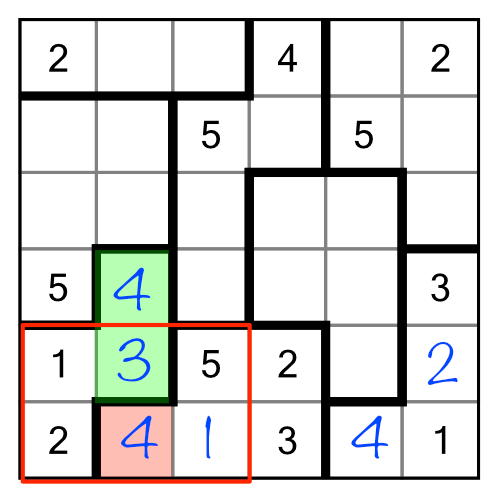
Once we’ve filled in the most obvious cells, we can move on to using an elimination strategy. Consider the region and cell highlighted:
At first glance this looks a little more complicated because now we have three cells within a region that we need to fill in. But actually we can apply the same logic to eliminate certain possibilities.
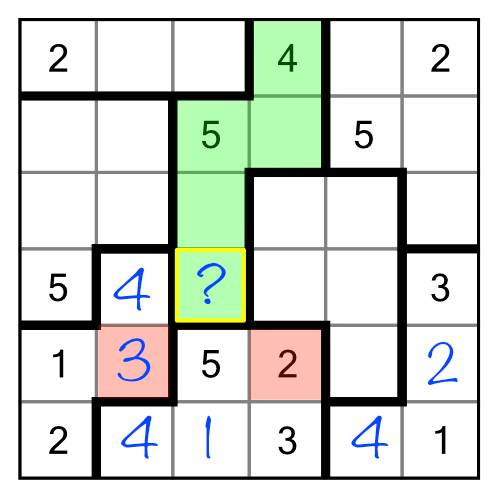
The red 3 and 2 prevent us from putting either of those numbers in our cell in question, which only leaves the 1.
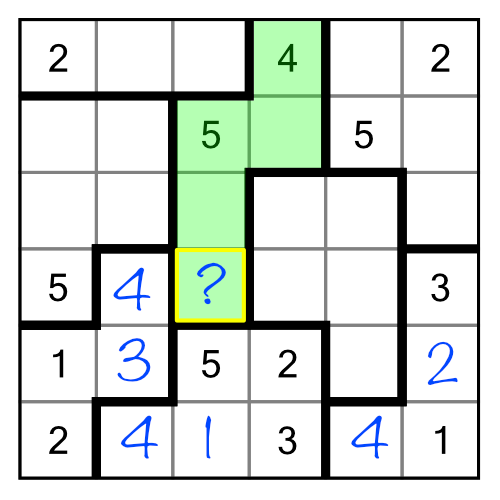
There’s another way we can use elimination, and it’s a bit more subtle. So far we’ve used pre-filled and solved cells to eliminate candidates. But in suguru we can also eliminate candidates based on implication. Consider the region with no numbers in it at all:
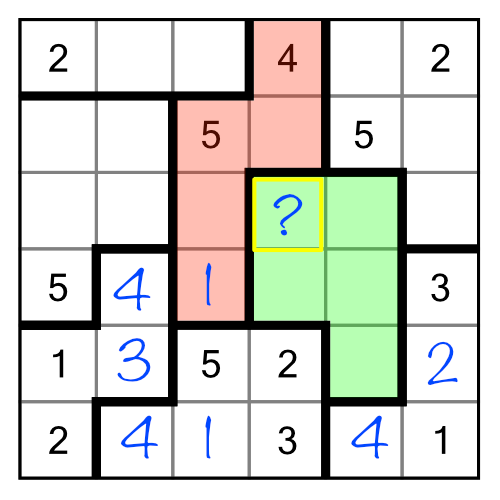
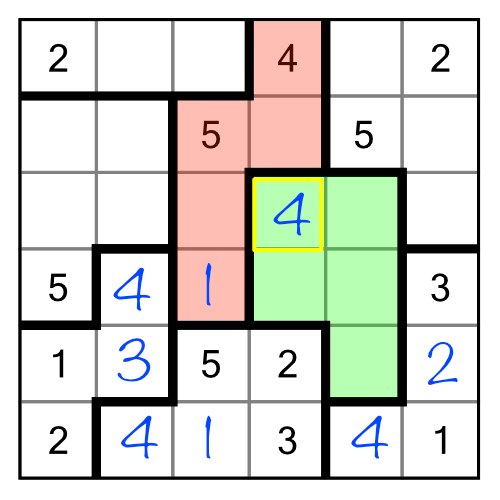
We know we need to find all the digits from 1 to 5 to fill this region. We can use the neighbouring (red) region to help us get started. The red region needs a 2 and a 3 in order to be completed. Given how our green region is partially surrounded by the red one, we can automatically eliminate 1, 2 and 3 as candidates for the cell with a “?” inside, and of course we can eliminate the 5 as well. Even if we didn’t already have the 1 and the 5 filled in inside the red region, we could still eliminate 1, 2, 3 and 5 based purely on implication. Putting any one of them into our “?” cell would make the red region impossible to solve! Therefore we can deduce that the only possible digit that can go there is 4.
That’s a simple example of elimination by implication, but it’s a powerful technique that can be used to solve regions that at first glance appear to have no clues to go on. To see how powerful, here's an example from a different puzzle:
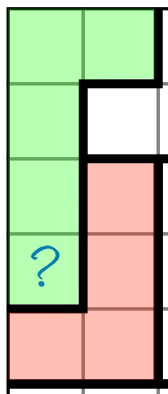
It looks like we have no clues at all to help us here, but of course that’s not true. There are certain things we do know. The green region has five cells, so requires the digits 1-5. The red region has four cells so needs 1-4. Elimination by implication tells us what the “?” cell contains. Given its position surrounded by the red region, it cannot contain a 1, 2, 3, or 4. If it did, it would be impossible to put any of those digits into the red region. Therefore it must contain a 5 - it’s the only option.
Looking back at our example puzzle, it can easily be solved now with simple elimination.
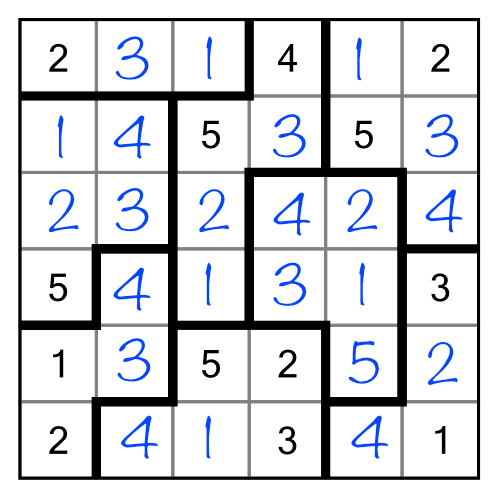
Just as with sudoku, writing in small numbers to show candidates for a cell can be a useful thing to do — especially on harder grids. It can ease cognitive load and show you opportunities that might not be obvious otherwise. Consider this puzzle:
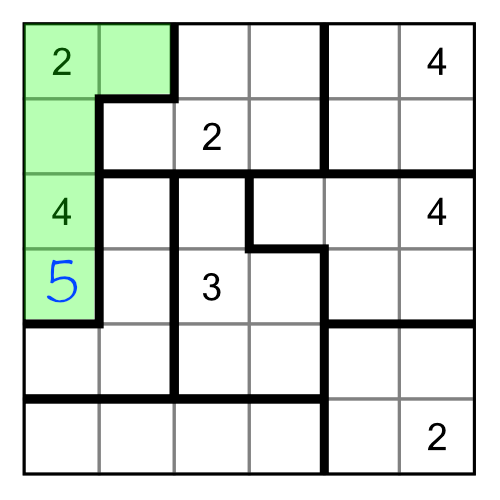
We’ve already solved the 5 in the green region based on elimination by implication. Where do we put the 1 and the 3 though? For now we don’t know, so we can write them in as little numbers:
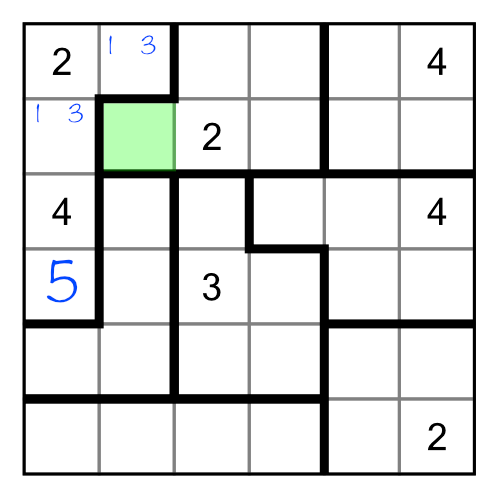
Now when we come to consider the green cell, we can immediately see that it cannot be a 1, 2, 3 or 4, so must be a 5. Yes, we could have worked this out without writing in the small numbers, but when working bigger puzzles with larger regions, taking notes like this can make it easier to spot answers as your notes will ripple out across the puzzle. When that happens, some combinations of notes will eliminate candidates in others, solving cells that then ripple back through your earlier notes.
Suguru is all about elimination. Elimination by implication can give you a quick ‘in’ to fill out some extra clue cells, helping you get started. Taking notes on harder puzzles will uncover hidden elimination opportunities.
If you find you get stuck in a puzzle, work through noting all possible candidates in the empty cells, and you will find pairs of candidates that, when combined, eliminate candidates from pairs of neighbours.
To help you practice, we’ve put together a set of easy level suguru puzzles you can print out, along with the solutions in a separate PDF. You can download both below.
If you enjoy suguru and would like enough puzzles to keep you going for an entire year, then our A Year of Suguru books are for you. Large grids, and a daily rotation through five levels of difficulty mean you’ll have a fresh challenge every day of the year. Choose from Easy-Intermediate and Intermediate-Hard editions.
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.
If you’ve never played killer sudoku but want to get started, or if you’ve taken a look at a killer sudoku grid and wondered how on Earth you’re supposed to begin solving it, then you’ve come to the right place.
Killer sudoku is like regular sudoku but with added mathematics. Unlike the classic game, there’s arithmetic involved. If that’s not your thing, killer sudoku probably isn’t for you!
A quick word of caution before we get started: killer sudoku is very much based on regular sudoku. You really need to know how to play the classic version before tackling this kind of puzzle. So if you’ve never solved a sudoku puzzle before, I would recommend reading through our Sudoku From Scratch guide, and doing some simple puzzles first (there are some free ones to download included in our guide).
With that said, let’s dive in and look at a killer sudoku grid, and the rules that govern the puzzle. Here’s an easy grid to start us off — it’s a 1-star grid from our Pocket Killer Sudoku range.
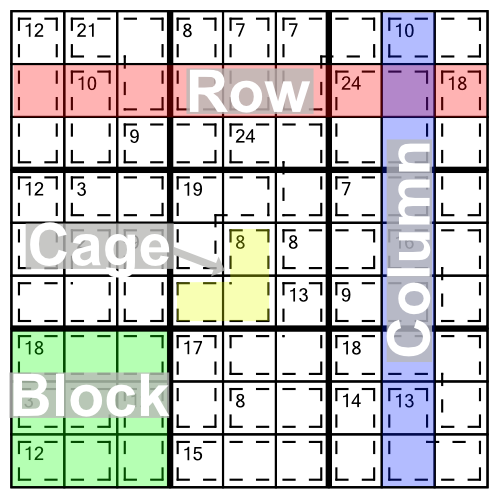
There are lots of things that are familiar about this grid if you are used to sudoku:
There are also a couple of very obvious differences between a killer sudoku puzzle and the regular variety.
The first rule of killer sudoku is the same as sudoku:
To this we add a new rule:
There’s the arithmetic; every killer sudoku puzzle involves a bit of adding up.
Looking back at our example grid above, we can see that the yellow cage has a little 8 written in the top cell. That means that the three numbers that go in that cage must add up to eight.
Whether you want to do your killer sudoku arithmatic in your head, or with the aid of a calculator, is up to you. But beware: any mistakes in adding up clue numbers will lead to errors that make the puzzle impossible to solve!
Solving killer sudoku puzzles requires a number of techniques. Some of those are the same as regular sudoku. Hidden and naked singles, single free cells, matching pairs and so on, all work exactly the same. But of course to use those we need to have some cells filled in, and when we begin a killer sudoku there aren’t any. So we can’t begin solving a killer sudoku puzzle the same way we would with a regular grid. We have to find another means of making headway. We need some specialist techniques, and that’s what we’re going to learn now.
When we add up all the digits from 1 to 9, we get 45. We can therefore deduce that the sum of every row in a killer sudoku grid must be 45, that the sum of every column must be 45, and the sum of every block must also be 45. How does this help us solve a puzzle? Consider our example grid again:
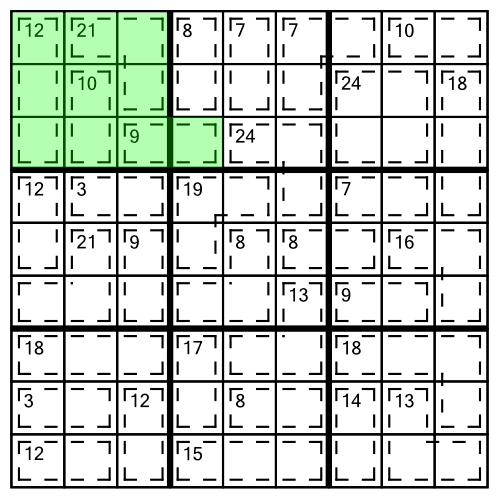
Looking at the top left block we notice that all but one of the cages are fully contained within it. The 9 cage spills over into the next block. We know that the sum of the block must be 45. We can add up the clue numbers (12+21+10+9) to get 52. That’s bigger than 45 - the maximum sum possible in a block. Therefore everything over and above 45 must fit into the single cell that spills out of the block. 52 minus 45 is 7, so that cell must contain a 7. Which in turn means the other cell in the cage has to be a 2:
Naturally we can use the same technique on rows and columns as well as blocks.
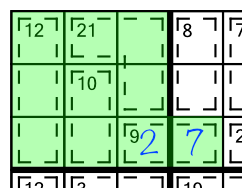
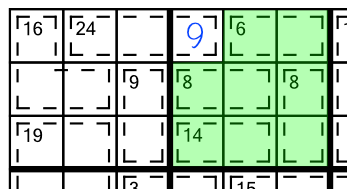
Sometimes cages don’t spill out out an area, they spill into one. Here’s an example from another 1-star grid:
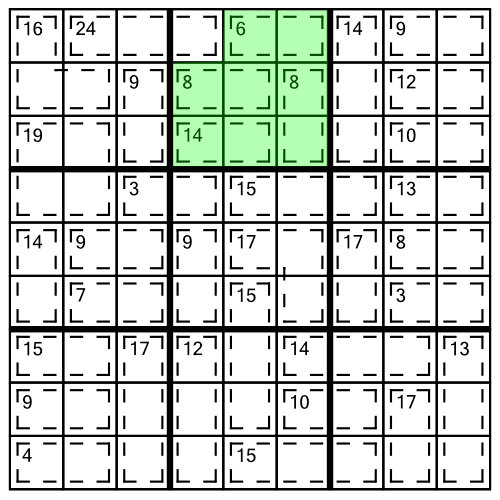
The principle is exactly the same. We add up the sum of the cages wholly contained within the block, to work out the value of the cell that has spilled into it.
6 + 8 + 8 + 14 = 36. We need all the cells in the block to add up to 45, so the cell that has spilled into it (the only one not shaded green), must contain a 9 (45 - 36 = 9):
Looking for places to apply this 45 rule is a good way to start a puzzle because it allows us to fill in some cells very quickly. Our example puzzles here are 1-star (easy) level. Harder puzzles won’t give up their secrets so easily. However, it’s worth keeping an eye out for places to apply this rule as you progress through a puzzle, because as cells get filled in, they can be used in the sum calculations, opening up more places to use this simple technique.
We can take the 45-rule further by applying it to multiple columns, rows, or blocks simultaneously:
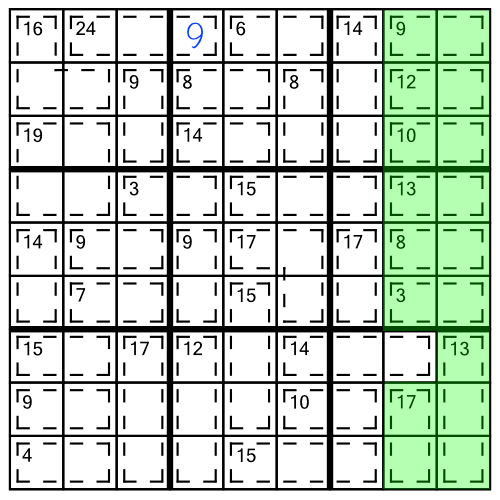
Neither of these columns alone are candidates for the 45 rule, but by combining them we find we have a single cell spilling inside. Working out its value is simple. We know the sum of the highlighted columns must be 90 (2 columns x 45). If we add up the clue numbers we get 85. Therefore the cell spilling into the columns must contain a 5, because 90 - 85 is 5.
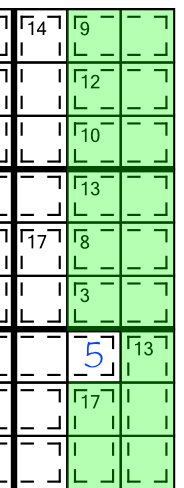
Here’s another example, this time combining three blocks together:
Adding all the clue numbers together gives us 137. As we have three blocks, we know the total should be 135 (3 x 45), so the extra 2 must go in the cell spilling out:
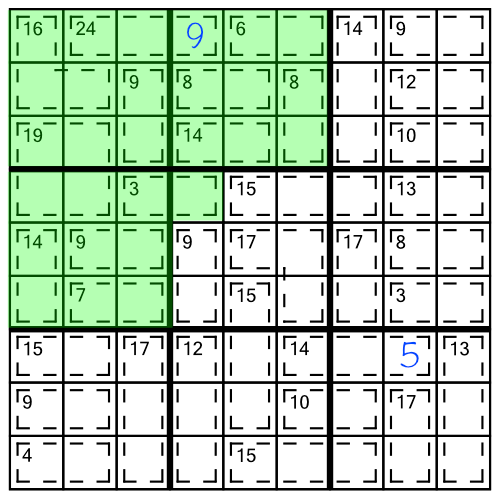
That in turn tells us we can put a 1 in the second and last remaining cell in that cage:
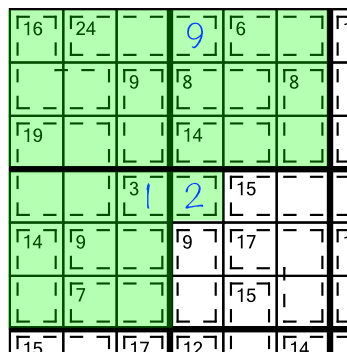
For any given cage, there are only a limited number of digits that can legitimately add up to its clue number. This block contains a cage with an 3 in it, and it’s made of two cells. For brevity, we notate this as a 3(2) cage.
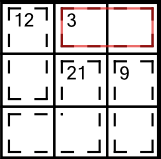
The only numbers that add up to 3 are 1+2. Therefore one of the cells must contain a 1 and the other must contain a 2. On its own this information doesn’t allow us to solve either cell definitively, but it narrows them down to two possible digits each, and we can write those in as little numbers, just like in sudoku:
We know from sudoku that matching pairs like this are very useful. This one allows us to eliminate the numbers 1 and 2 from the rest of the row and and the rest of the block.
Now let’s consider the example of an 8(2) cage (so that’s a two cell cage with an 8 written in it). Here are the possible combinations of numbers that could go in those cells:
Why not 4 and 4? Because no two cell cage could possibly contain the same digit twice — it would mean putting the same digit twice into a column or row.
Knowing that each cell in an 8(2) cage could contain a 1, 2, 3, 5, 6 or 7 isn’t very useful. But other cages are much more restricted - as was the case with our 3(2) example earlier. To save you working out other combinations yourself, here are all the two-cell cages that can only contain two digits:
If you want to see the limited sum combinations for larger cages, take a look at our killer sudoku cheat sheet.
There are certain sum combinations that always contain certain digits. For example, our yellow highlighted 8(3) cage right at the top of the page could comprise any of the following:
Knowing that any of the three cells in the cage could contain a 1, 2, 3, 4 or 5 is not very handy. But knowing that one of them must contain a 1 is much more useful. It allows us to write a little 1 into each of those three cells, thus eliminating it from the rest of the block.
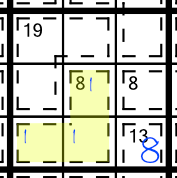
We’ve put the required digit sums into our cheat sheet too, to save you some more time. As with limited sum combinations, learning some of these by heart is a sure way to speed up your solving skills.
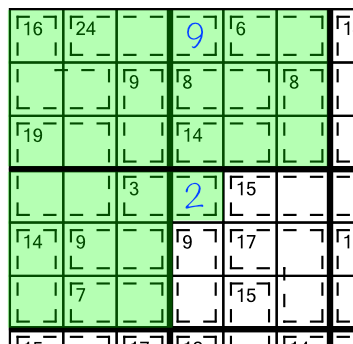
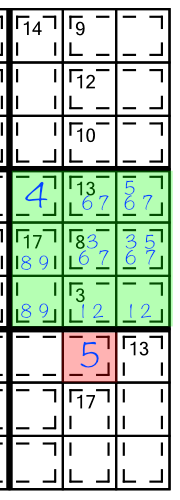
We can push a puzzle a long way just by combining the techniques we have looked at so far, along with using what we already know about sudoku. Let’s work through a quick example. Consider the middle block of this right-hand stack:
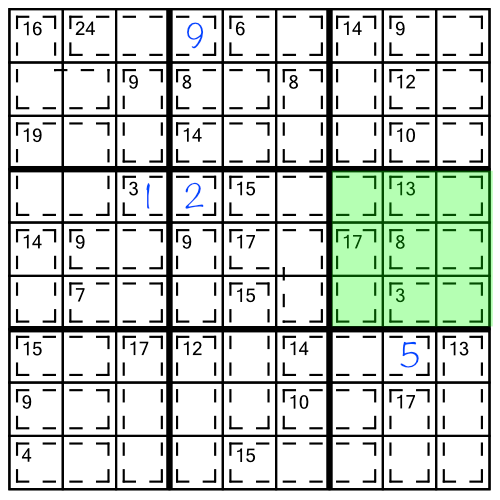
The first thing we can and should do, is work out the contents of the cell from the 15(3) cage that is spilling inside this block. Adding up the cages wholly contained in our block yields 41, so the intruding cage's cell must contain the missing 4 to bring us up to the requisite 45.
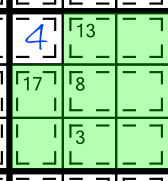
Next, based on what we know about limited sum combinations, we deduce that the 17(2) cage can only contain an 8 and a 9. And we can also work out that the 3(2) cage can only contain a 1 and a 2. Look what happens when we write in those little numbers:
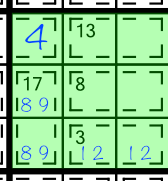
Knowing that this block already has the digits 1, 2, 4, 8 and 9 taken care of, reduces the possible candidates for the other cells. So whereas an 8(2) cage could normally take candidates 1,2,3,5,6 and 7, here we can reduce that list to 3,5,6 and 7. And in fact if we zoom out and look at the stack again, we notice that there’s already a 5 in the middle column, so we can reduce the options even further in half of the cage.
The same logic applies to the 13(2) cage. Normally it could hold a 4,5,6,7,8, or 9. Given what we know must already be in the 17(2) and 3(2) cages, and the cell that’s already filled in, we can reduce those candidates to 5,6, and 7. And again, the 5 already in the column reduces the options further in the first cell in that cage:
Working across the puzzle in this way, combined with regular sudoku techniques, is enough to solve easy-intermediate puzzles like the examples presented here.
The key to solving easy killer sudoku puzzles is to use all the tools we’ve covered, to eliminate possible candidates. Often you will find that you can reduce and reduce the possibilities within a cage so far that you solve one cell in the cage. That in turn reduces the possible candidates for other cells within the same cage, and so on.
Remember to always look at the repercussions of each cell you solve — in killer sudoku even more so than in regular sudoku, solving a single cell can have huge repercussions that ripple out across the whole puzzle.
What starts off as a seemingly impenetrable grid, can very quickly evolve into something that becomes easy to solve as you combine the killer sudoku sum clues with regular sudoku techniques.
If you want to practice solving 1-star puzzles, we’ve put together a set you can download and print out below, as well as the solutions to check your answers. And of course, we have a full range of high-quality killer sudoku books, including our popular A Year of Killer Sudoku - with a new puzzle every day for a year.
Killer Sudoku Practice — Grids
Killer Sudoku Practice — Solutions
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.
In part one of this tutorial we began by looking at the basics of sudoku, using smaller than normal puzzles. Part two took us through using racks and stacks to solve 1-star level full size puzzles. Now it’s time to ramp things up to the next level - literally.
We’re going to look at a 2-star grid and learn a couple of techniques that will help you solve puzzles faster, and prepare you for even higher-level puzzles along the way.
If you’ve arrived here without any knowledge of sudoku, I’d highly recommend going back and covering those earlier sections first - everything here will make a lot more sense that way.
Here’s a 2-star puzzle, taken from our Pocket Sudoku — Classic range:
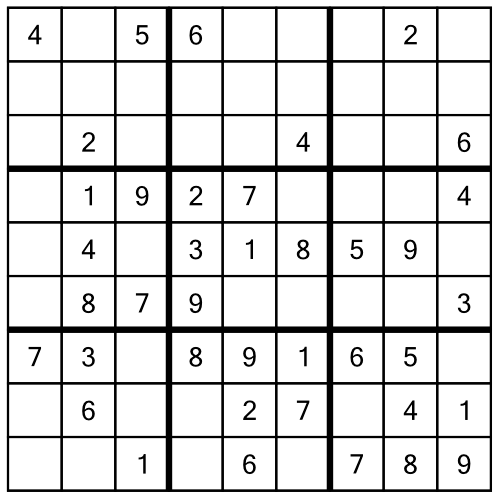
If you want to follow along yourself, you can download this grid to print out at home here.
A quick glance at the puzzle tells us there aren’t any easy single free cells to fill in - every row, column, and block has at least two empty cells. So we begin by working the racks and stacks. This time I’m going to do the racks first, because why not? There’s no right or wrong way to attack a sudoku puzzle.
Working across the top rack, we can fill in a 2 and a 4. When we get to the 6, there are two possible cells it could go in:
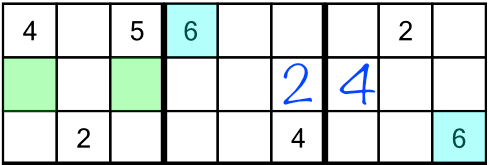
We could move on and look for the next number — it’s what we did back in part two of this tutorial in situations like this. But there’s a better way. Instead, we will write a tiny little number 6 in both the candidate cells, like this:
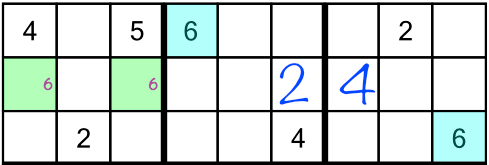
You’re probably wondering how this will help. Don’t worry, we’ll come on to that in a bit. First though, here’s some sudoku etiquette about how to write in little numbers. It’s best to always write them in the ‘correct’ place within a cell, because as we work through the puzzle we may end up putting more than one little number in a cell. Just jotting them down willy nilly will make our puzzle messy and hard to read. It’s better to have a system. To figure out where to write little numbers, just imagine the cell is filled with all the possible values, like this:
Sticking to this convention really makes working with the puzzle easier. By the way, it’s best to use pencil for solving sudoku puzzles because later you’ll want to erase the little numbers. It’s also good to have cells big enough to put several little numbers in without having to write microscopic digits. It’s why all Puzzle Genius sudoku books have generous sized grids - even our popular Pocket Sudoku range.
Back to our puzzle. There’s nothing more we can do with the top rack, so we move on to the middle one. Straight away we see that we have two candidate slots for the 1, so we can write in two little numbers:
Working through the rack we can fill in the 3, 4, 7 and 8. This is what the grid looks like so far:
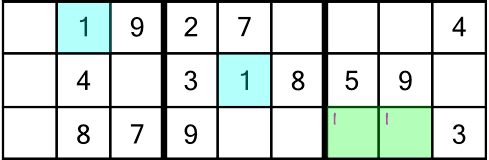
On to the third rack. The first opportunity we have to write anything in is the number 8. Again we have two candidate cells. We write in the little numbers, like this:
Now look what happens when we reach the number 9:
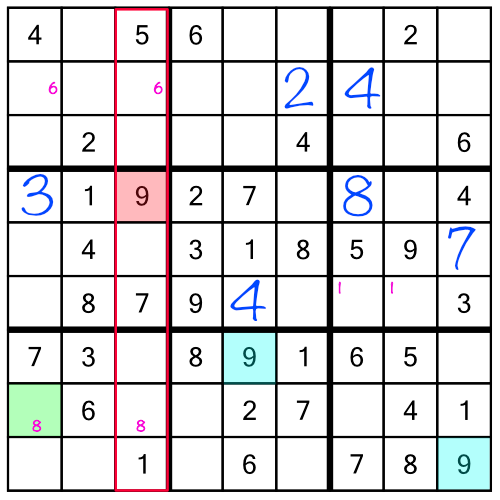
There’s a 9 in the middle block and top row (of the third rack), and there’s a 9 in the third block and bottom row. Logic tells us we have to put a 9 in the first block and middle row of the rack. There are two empty cells to consider, but one of them is out of bounds because there’s already a 9 in the column that cell is in. That leaves just one candidate cell, and it already has a little number 8 inside it. Remember, those little 8s are there to tell us one of the two cells must contain a number 8. When we write our 9 into the green cell (the only place it can go), we are ruling out the possibility of an 8 going in there:
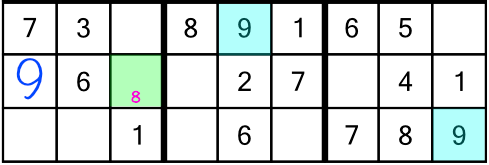
Now the only place left to put our 8 is the one remaining cell with a little 8 in it. Writing in the little numbers earlier meant we got to solve two cells in one go!
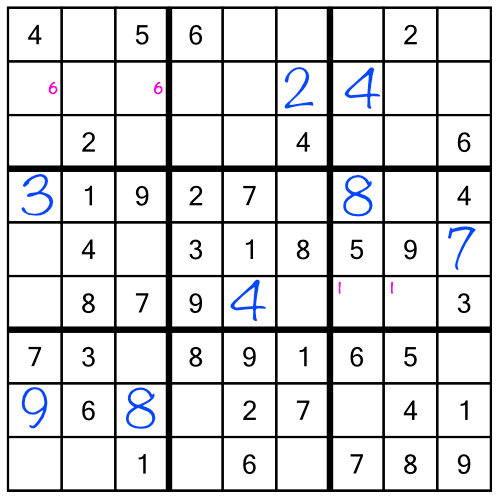
We would have found the 8 eventually, even without the little numbers. Our second tour through the racks — after we had worked through all the stacks — would have shown us where to put it. But doing it this way means we got to fill it in much earlier, saving us time and potentially making it easier to work through the stacks, because every completed cell makes the puzzle a little bit easier.
There are more benefits to using little numbers, and we’re going to cover one of those right now, as well as learning another technique that can speed up our sudoku solving powers!
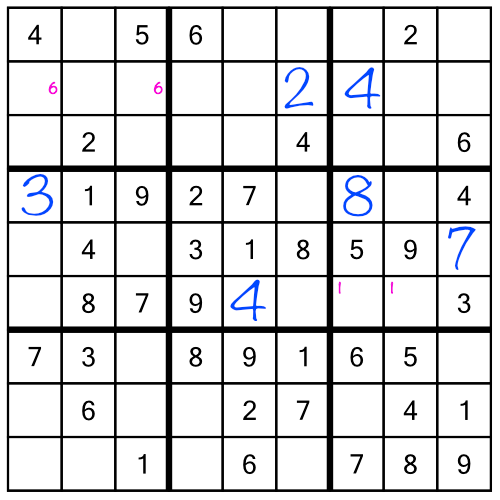
Let’s continue with our example puzzle. I’ve gone ahead and worked through the first stack, and the middle stack as far as the number 8. This is what the grid looks like so far:
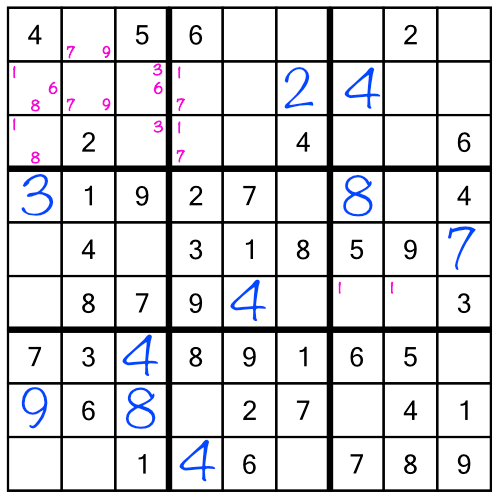
It’s starting to get a bit crowded - but don’t worry, all those little numbers are going to be a great help. Starting right now, when we add in the number 9 in the middle stack:
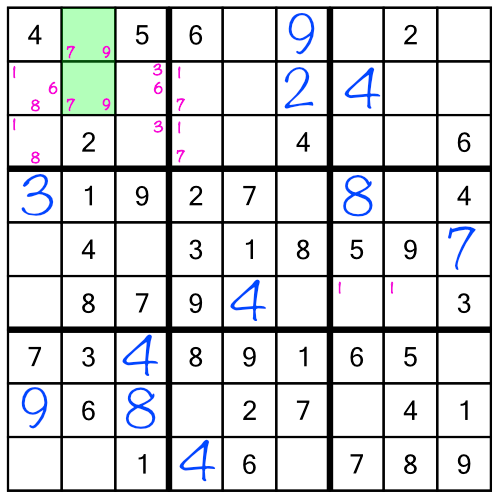
Looking back at the top left block, we notice the green cells both contain a little 7 and a little 9. When two cells in the same row, column, or block, contain two — and only two — little numbers, that tells us that they can only hold one of those two numbers. In other words one of those green cells must be a 7, and one must be a 9. There are no other numbers that could go there. And now that we’ve just filled in that 9 in the top row (middle stack), we’ve ruled out the possibility of the top green cell holding a 9!
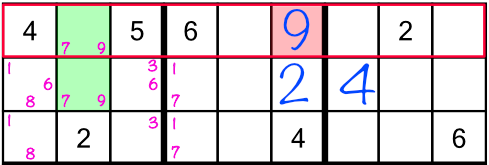
The repercussion of filling in the 9 in the top block of the middle stack is that now we know which green cell holds the 7 (the top one) and which holds the 9 (the bottom one):
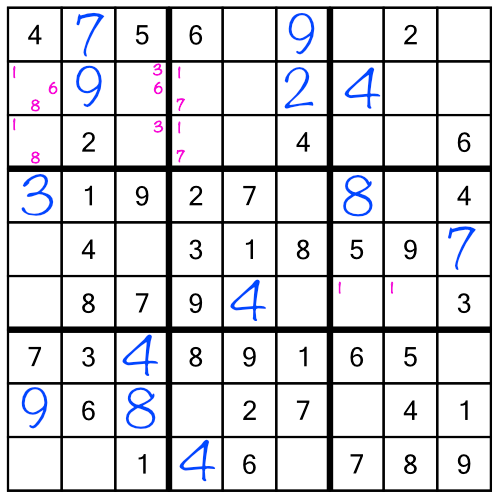
Repercussions are an amazing way to solve puzzles more quickly. The technique is simple: every time we fill in a cell definitively (that is to say with a full size number, not a little number), we look at the puzzle to see if that number helps us solve any other cells. The repercussion of filling in the 9 in the middle stack was that we could solve the 7 and 9 in the left stack.
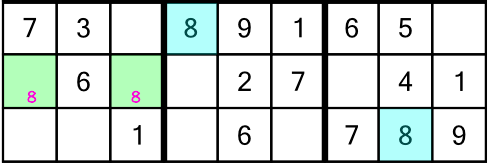
Before we move on working to the last stack, we can see if the 7 and 9 we just solved have any repercussions themselves
The 7s in the left stack are already all solved, and we don't have enough information to solve the 7s in the rack. But guess what? The new 9 means we can solve the third 9 in the top rack:
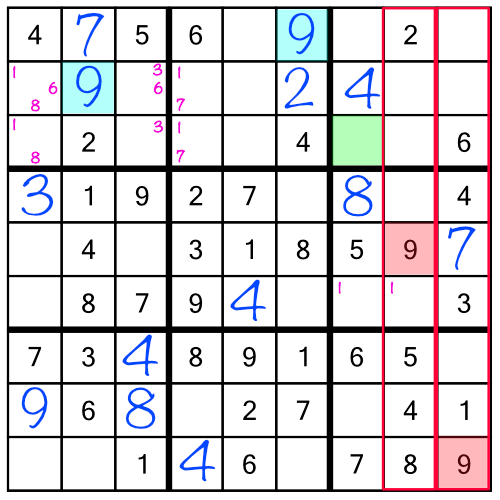
Now we've solved all the 9s in the puzzle. But that’s not the only repercussion. The 7 and 9 we added earlier have given us a single free cell in a column:
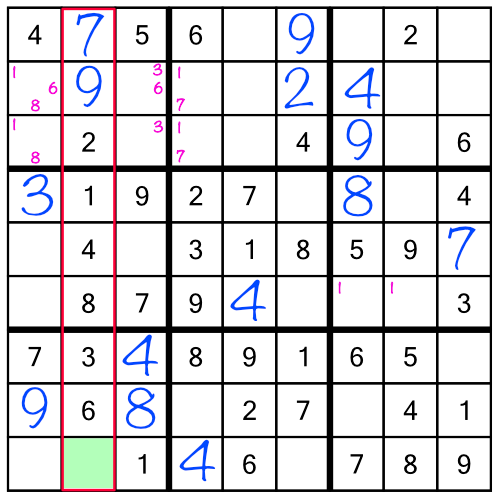
Filling it in with the number 5 gives us three more repercussions:
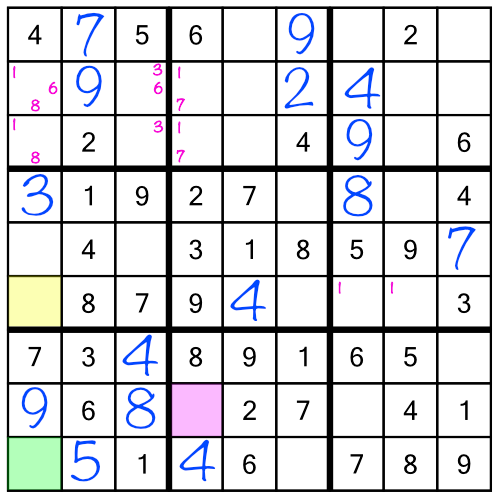
Filling in those numbers in turn gives new repercussions, and so on as the empty squares fall like dominoes. In fact, just by following the repercussions, we can solve the whole puzzle! We don’t even have to work through the final stack, and we certainly don’t need to work through the racks a second time.
Why not try and complete the rest of the puzzle yourself? When you are ready, you can download the solution here.
You now have enough techniques under your belt to solve 1 and 2-star puzzles, and with a bit of effort some harder ones too. There are plenty more techniques to discover though, and filling in those little numbers is key to making many of them work.
If you want to practice solving 2 star puzzles, we’ve put together some 2-star puzzles you can download and print out below, as well as the solutions to check your answers. And of course, we have a full range of high-quality sudoku books, including our popular A Year of Sudoku - with a new puzzle every day for a year.
9x9 Sudoku 2-Star Practice — Grids
9x9 Sudoku 2-Star Practice — Solutions
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.
In part one of this tutorial we began looking at sudoku from the first principles. If you’ve never tried sudoku before, we’d recommend going back and reading that page because it covers the basic foundations.
Here in part two we are going to move on to full-sized 9x9 grids - the kind you’ll find in most books, including ours (though we do have some bigger versions for the more adventurous).
Here’s an empty 9x9 sudoku grid:
It’s just like the little 4x4 grid we looked at before, only bigger. The grid uses all the single-digit numbers from 1-9. Each row, column, and block must have each number 1-9 once, and only once.
Now let’s look at a real puzzle. This is an easy one - a one-star puzzle from our Pocket Sudoku - Classic range.
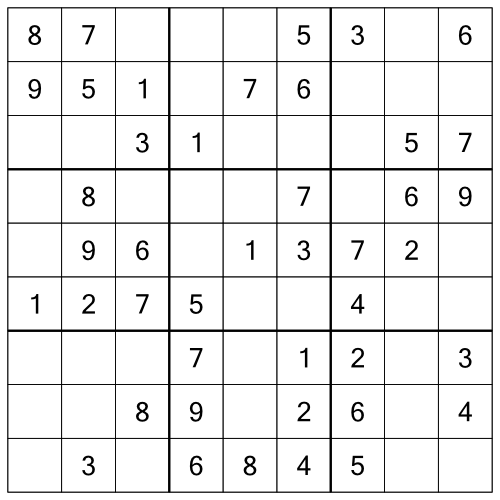
If you are new to sudoku, then at first glance a puzzle like this can look a bit intimidating. All those empty cells! What’s more, on closer inspection you might notice that unlike the little grids we looked at in part one, this one doesn’t have any rows, columns, or blocks with just a single empty cell.
Fear not. This really is an easy puzzle, and we’re going to deconstruct it to see why.
When we say deconstruct, we mean literally. We are going to break the puzzle apart and turn it into smaller bite-sized chunks that are much simpler to solve.
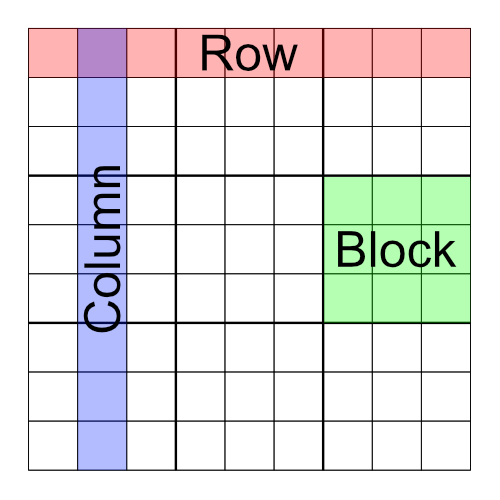
There are two ways we can break apart a sudoku grid. The first is by splitting it into three equal parts horizontally, along the thick lines, like this:
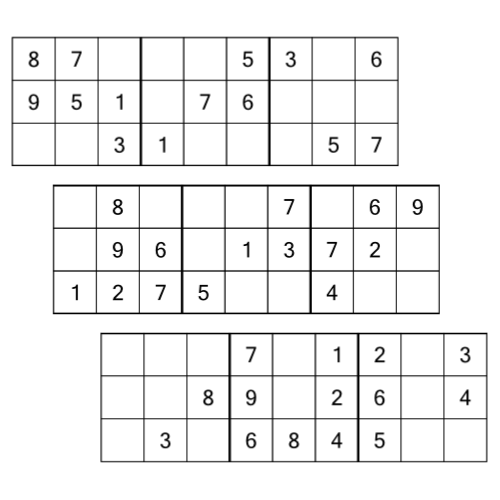
We call each of these horizontal sections a rack. As with everything in sudoku, different puzzle designers have different names for things. Rack is pretty common, and it’s what we stick with here at Puzzle Genius, but you might see racks referred to as ranks or even (confusingly) rows, in other places.
Looking back at the original grid above, you’ll see there are thicker lines running top to bottom as well. Splitting the grid vertically along those gives us three stacks, like this:
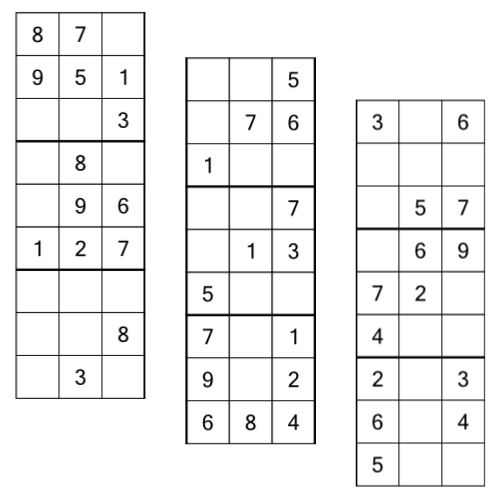
Again, different folks may have different names. We stick with stacks.
Now obviously we aren’t going to physically cut out a sudoku puzzle and chop it up like this. But thinking of a grid as smaller racks and stacks makes it easy to tackle the puzzle because we’re only looking at three rows, columns, or blocks, at a time
To see how using racks and stacks is helpful, let’s work through our example puzzle, starting with the top rack.
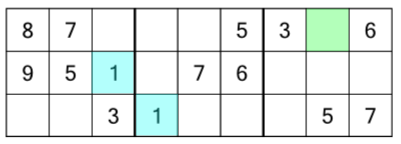
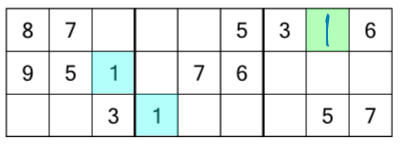
Step one of solving this grid is to look at where all the number 1s are in this first rack. There are two of them already filled in for us (highlighted here in blue). The first is in the first block and middle row. The second is in the second block and bottom row. We know every block and every row has to contain every number, once. So in this rack, logic tells us we need to put a number 1 somewhere in the third block, and somewhere in the top row. And guess what? There’s only one empty cell that falls in both the last block and top row. We have to put a 1 there. Like this:
We can repeat this step, this time looking for number 2s. But there aren’t any number 2s in this rack, you say. And you’re right! No need to worry, we can move on and look for number 3s.
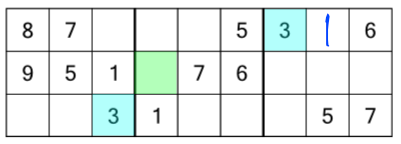
There’s a number 3 in the first block and bottom row, and one in the last block and top row. We must be missing a number 3 in the middle block and middle row. And again, there’s only one empty cell in that block and row (the green one), so we have to put a 3 in it, thus ensuring each row and block has a single number 3.
As you’ve surely figured out by now, we look for number 4s next, but there aren’t any. The number 5 already appears in each row and block, so we move on to the 6s. And here we have a bit of a problem:
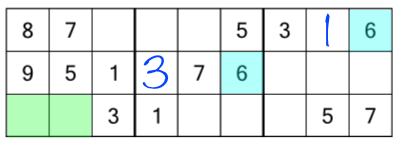
There are two 6s, and logic has narrowed down the possible homes for the third to two cells. Which one is correct? Right now we don’t know. We never guess in sudoku, because if we get it wrong we won’t know straight away and by the time we realise there’s an error in the grid, it will be far too late to work out where we made a mistake and we’ll have to start over. What then, are we to do? Simple: we carry on looking for the next numbers. We’ll come back to the 6s later. Right now we can check the 7s (they are all present already), and then the 8s:
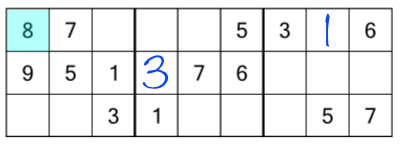
There’s only one 8, so we can’t draw any conclusions about where to put the others yet. The same is true of the 9.
We’ve done all we can with this top rack (for now), so we can move on to the second rack and repeat the process.
There’s a 1 we can fill in in the top row of the rack, but the 2s are inconclusive, and we don’t have enough 3s, 4s or 5s to work those out yet. Once again, the 6s present us with a minor dilemma:
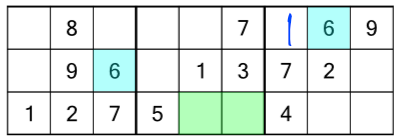
With a 6 in the middle row and first block, and one in the top row and last block, we know we have to add one somewhere to the bottom row and middle block. There are two empty cells there, but unlike the first rack, this time we can work out which is the correct place. How? By looking at the puzzle as a whole again:
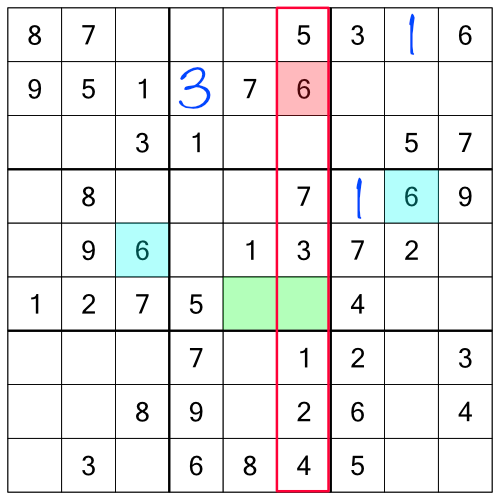
Looking at the entire grid allows us to consider not just the row and block, but also the column. And look - of the two cells we could consider for the 6, one of them is in a column that already contains a 6, so we know we can’t put it there. That only leaves one possible place for our missing 6:
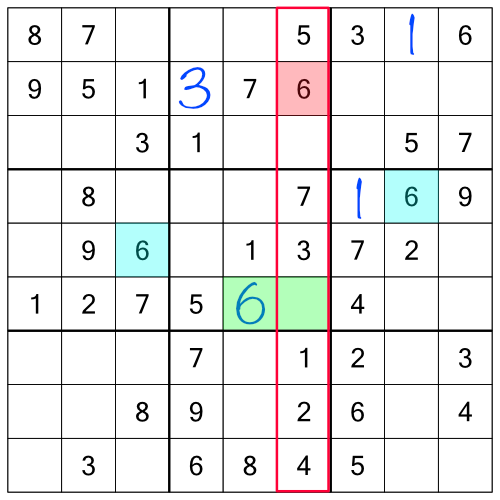
The 7s are all present and correct, and we only have one 8 so can’t do anything with that. The 9 in the middle row and the 9 in the top row tell us we need to put a 9 in the bottom row (middle block), and now we've only one free place to put it, so we can fill that in:
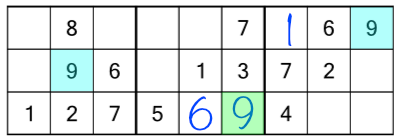
We do the whole process again for the bottom rack, where we find a missing 3 and 8.
This is what the grid looks like after working through the three racks:
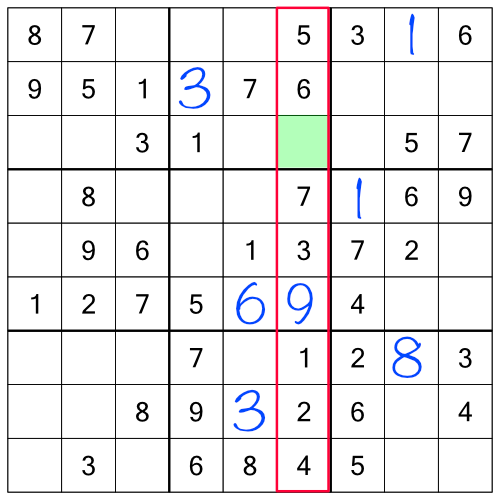
Working through the racks has allowed us to fill in enough empty cells that there’s now a column with just one number missing - a nice easy one to fill in. We also have an easy block to complete:
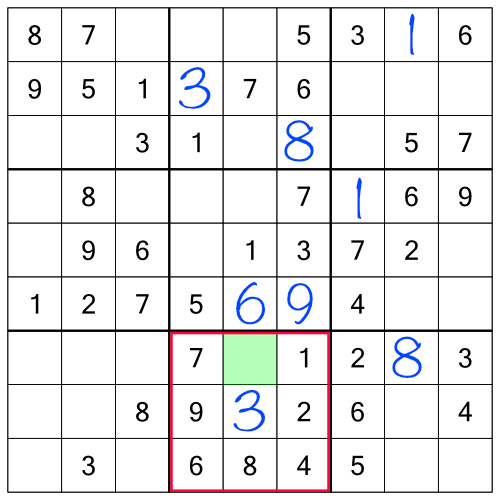
Here’s what the puzzle looks like so far:
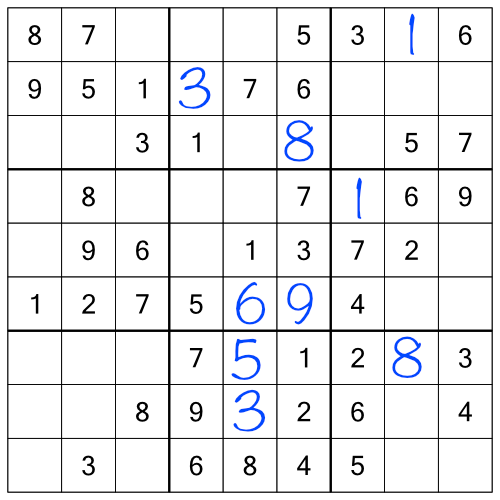
With the racks done, we can turn our attention to the stacks. The principle is exactly the same - take each stack in turn and work through the numbers to see what we can fill in. First up, the 1s in the left-most stack:
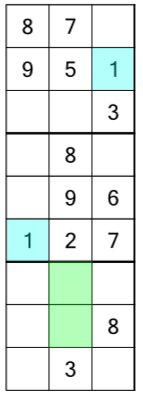
With a 1 in the top block and right column, and another in the middle block and left column, we know we have to find a place to put a 1 in the bottom block and middle column. There are two free cells there, so which do we go with? Once again, we can look at the whole grid to tell us:
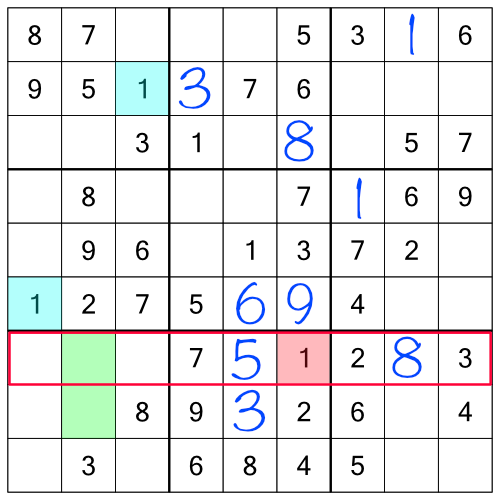
One of those rows already has a 1, so that only leaves one possible empty cell to put our missing 1.
After going through all the stacks using everything we’ve learned so far, our grid looks like this:
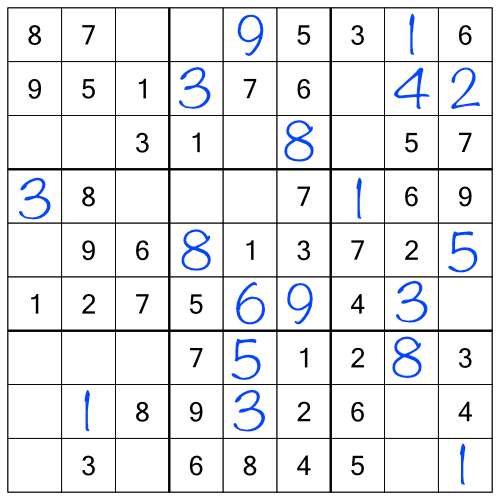
We’ve made some impressive progress, but obviously we’re not done yet. So how do we move forward? We could go back and go through the racks again. Having added in some extra numbers by working the stacks, we will almost certainly find that re-doing the racks will yield more answers. Indeed repeatedly working through racks and stacks might get us all the way to the end.
Before we do that though, looking at the puzzle as a whole shows us there are some easy cells to fill in - single free cells within rows, columns, blocks, or a combination:
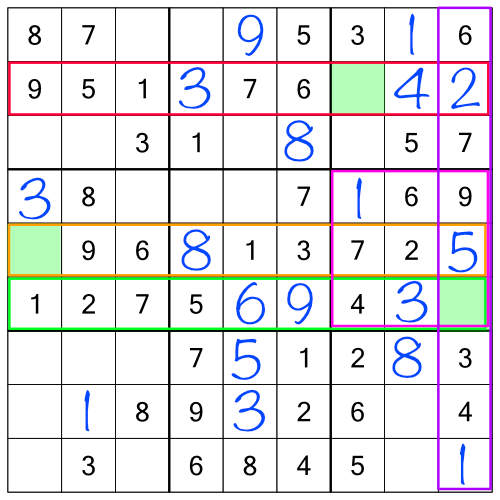
Filling all of those in makes the grid look like this:
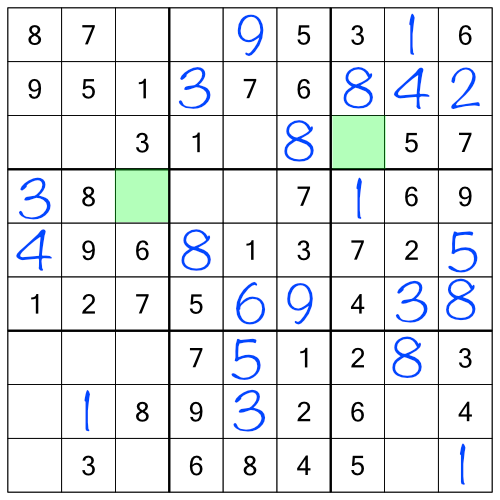
Now we’ve got even more single free cells to fill in. I said this was an easy puzzle! If we filling those, we get to this:
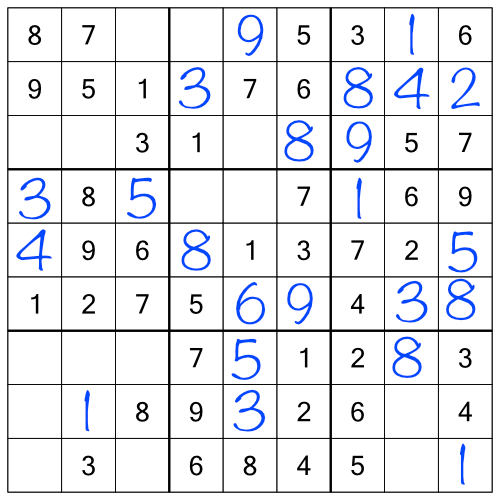
With no more single free cells, we can go back and work the ranks and stacks. At this late stage in the puzzle, we’ll find that often filling in a number as we work through the racks and stacks provides us with some easy single free cells we can fill in as well along the way.
Following everything we’ve covered so far, by re-working the racks, stacks, and single free cells, we can quickly complete the puzzle.
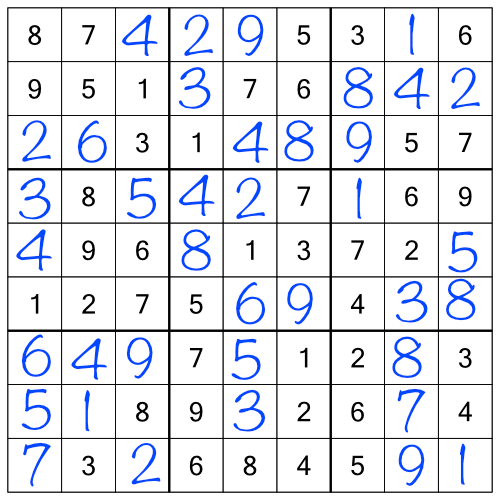
Congratulations! You now know enough sudoku to complete easy-level puzzles. Of course, there’s more to sudoku than just checking racks and stacks. Anything harder than easy-level grids will require some extra techniques.
To reach intermediate level, we are going to have to take things a little further. Part three of this series dives into a new technique that will take your sudoku-solving skills to a whole new level.
In the meantime, if you want to practice what you’ve learned so far, we’ve put together some easy puzzles you can download and print out, along with the solutions in a separate PDF.
And of course, we have loads and loads more puzzles in our books. Our Pocket Sudoku - Classic series is perfect for beginners. With five different levels of difficulty, you’ll find plenty of easy puzzles like the example we’ve just looked at. And as you learn more techniques, the higher levels will keep you busy too. All in a beautifully decorated, pocket-sized book you can slip into a pocket or bag and take anywhere.
9x9 Sudoku Easy Practice — Grids
9x9 Sudoku Easy Practice — Solutions
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.
If you’ve never played sudoku but want to get started, or if you’ve ever looked at a sudoku grid and found it intimidating or impenetrable, then you’ve come to the right place! This tutorial series assumes zero knowledge of the popular puzzle game. We’ll take you from scratch to being able to solve most puzzles up to intermediate level.
Sudoku is great fun, and is actually really easy to learn. It’s a good way to relax, to keep your mind sharp, and can be the perfect distraction from the difficult times we find ourselves in.
Contrary to popular belief, sudoku is not a mathematical puzzle. That it uses numbers is almost incidental. The numbers are just symbols, and in fact any kind of symbols can be used. Some kids sudoku grids use shapes or icons. Some sudoku puzzles use letters (these are usually called wordoku). Numbers are by far the most common symbol used in sudoku though, so that’s what we will stick with here.
The aim of the game is very straightforward: to find all the missing numbers in a partially filled grid of numbers.
To get started, we’re going to begin with a smaller than usual grid of numbers. It makes it easy to grasp the rules. What’s that, you say? What are the rules? Great question!
The rules of sudoku are encapsulated in its name, which comes from the Japanese Sūji wa dokushin ni kagiru, which means the numbers must be single. In sudoku, each number in a grid can only appear once in each row, column, and block.
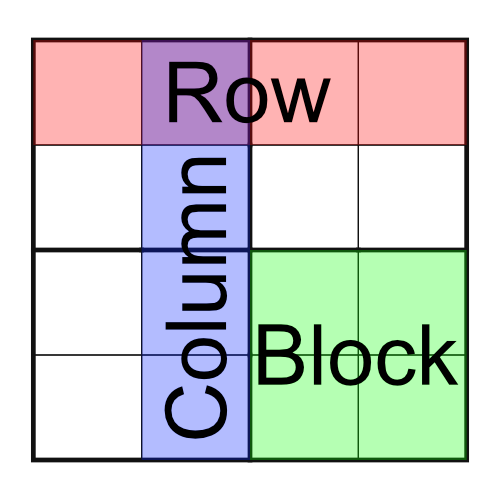
Before we go any further, let’s look at what a grid looks like, and explain some of that terminology.
Here's an empty sudoku grid. We call this a 4x4 grid because it’s four cells across and four down. Small grids like this are great for kids.
Note: If you have kids who you think would enjoy sudoku, we recommend Amelia Baker’s excellent Sudoku For Kids series. It starts with small grids like this and works up to full size ones, with fun tutorials along the way. It’s all wrapped up in a beautifully decorated book that kids will love.
The grid has four rows (each comprising four cells), four columns (of four cells), and four blocks - also made up of four cells. Some sudoku designers refers to blocks as boxes regions, or if they want to get really fancy, nonets. At Puzzle Genius we prefer to stick with calling them blocks because, well, they’re kind of blocky.
Here’s a 4x4 grid with some numbers filled in:

The aim of the game of sudoku is to fill in the empty cells with the missing numbers. We can always do this with logic - there’s no need to guess. In fact, guessing is very bad and should never be part of solving a sudoku puzzle. That’s because if we guess at the contents and get it wrong, we won’t necessarily know until we are much further into the puzzle. By the time we realise something is wrong, we won’t know where our mistake occurred and the only way forward would be to start over from the beginning.
Remember that sudoku comes from the Japanese for the numbers must be single? That means that:
Armed with the numbers already present, and these simple rules, we can solve the puzzle.
With a tiny grid like this, the logic to solve the puzzle is almost self-explanatory. But let’s lay it out there anyway, because making sure we understand the basics means we’ll have a good foundation for solving bigger, more complex grids.
The easiest place to start is with a part of the grid that’s already almost complete. Looking back at our example, which is super-simple, there are a few places we could begin. Let’s take the highlighted column which only has one number missing:
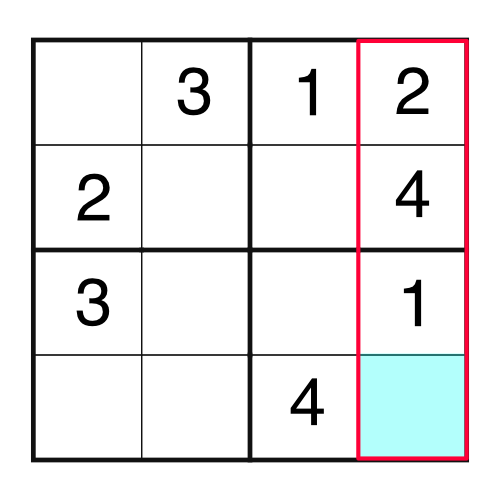
Given that column already has a 1, a 2, and a 4, the missing number is a 3. It’s the only number that can go in the blue square. We can write the 3 like this:
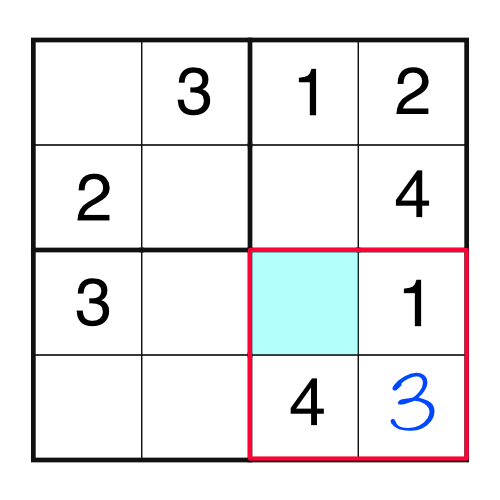
Now we have a block that’s only missing one number - the 2. Writing it in makes something interesting happen:
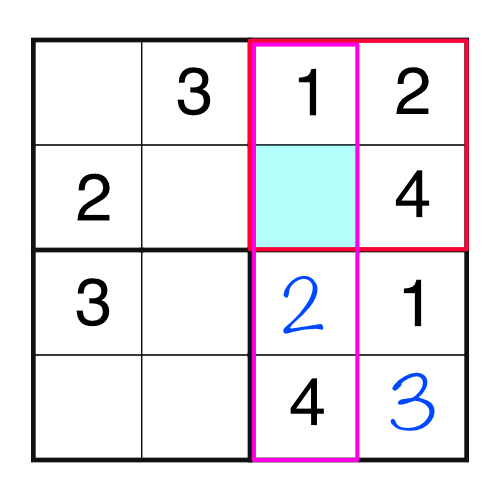
Look at that - there’s a block and a column that are both missing the same number. Fortunately they are missing the same number - the 3. If they were missing different numbers we would know we have a problem somewhere, because we’ve only got space to put one. Here’s what the grid looks like now:
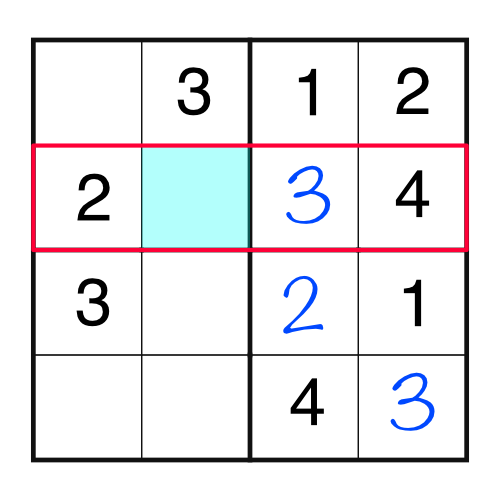
The next number is a 1:
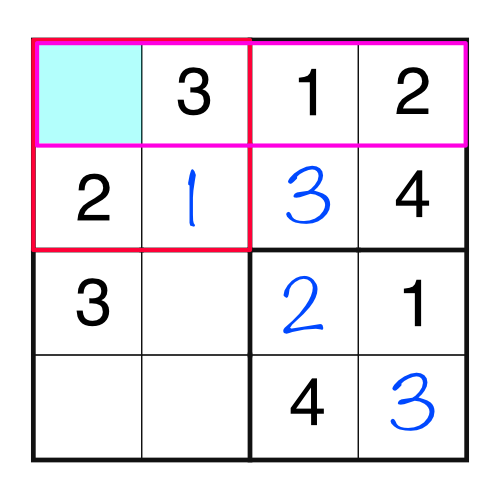
That gives us a block and row with the same empty cell, which has to be a 4.
It’s easy to keep filling in the single missing number each time until the whole grid is filled in. This is what the final solution looks like:

This example took one route to solving the puzzle, but it wasn’t the only route. There are no rules that say we had to start with the right-most column. It would have been just as easy to start with the top row, or the top-right block. In a puzzle this simple it’s possible to start in almost any cell. There’s no right or wrong way to proceed.
The sudoku puzzle has been completed, but are we sure we got the result right? Checking it is easy - we just have to apply the rules of sudoku to each row, column, and block. Working top to bottom, we can read off each row to make sure that they all contain the numbers 1-4 once and only once. Then we can work left to right doing the same for the columns. Finally we can triple check everything is hunky-dory by verifying each of the blocks also contains each number once and only once.
Sales pitch alert! Checking 4x4 puzzles takes seconds. Checking regular sudokus, which are 9 cells by 9 cells, takes longer. That’s why every Puzzle Genius puzzle book contains complete solutions at the back, to make it much faster to check your results.
The example we’ve just looked at was unusually easy. If every sudoku was that simple, the game would be very boring indeed. Let’s look at a more realistic puzzle, though we’ll stick with a 4x4 grid for this introductory tutorial.

This time there are no rows, columns, or blocks that are missing only one number. The best we can do is the block on the top left, which is missing two.
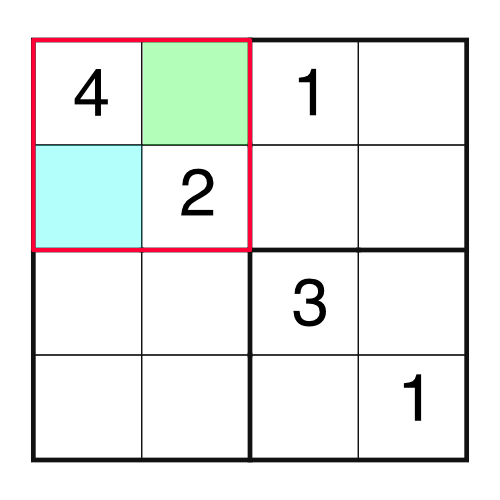
Logic is our friend. We have a 4 and a 2 in the block, which means we are missing a 1 and a 3. Which one goes in which empty cell? It’s easy enough to work out by considering other parts of the grid. For example, if we were to consider the top row, we would notice this:
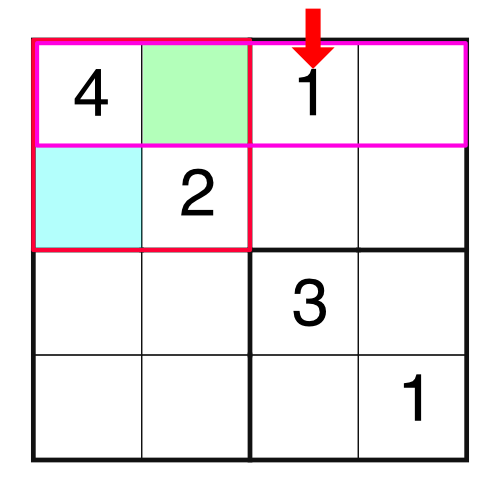
There is already a 1 in the top row, and we know we can’t put the same number into a row twice. That means we can’t put a 1 into the green square - we’d be breaking the rules. Therefore the only place the 1 can go in our highlighted block is the blue square.
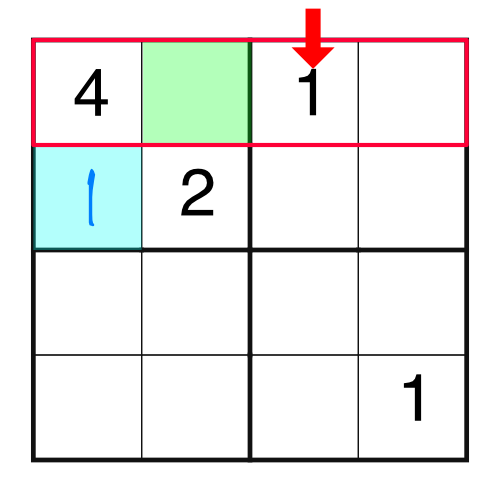
Now that block is only missing a 3, so that’s what goes in the green square.
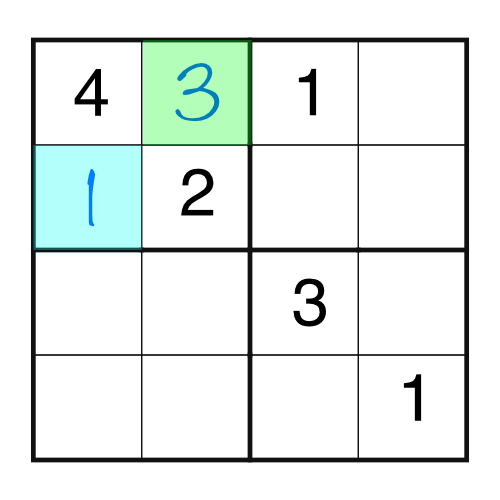
That little bit of login has opened up the puzzle. By filling in single missing cells we get to this stage.

At first glance, an entirely empty block might be difficult to solve. But it’s only a problem if we consider the block in isolation. Taking into account the rows and columns makes it a doddle.
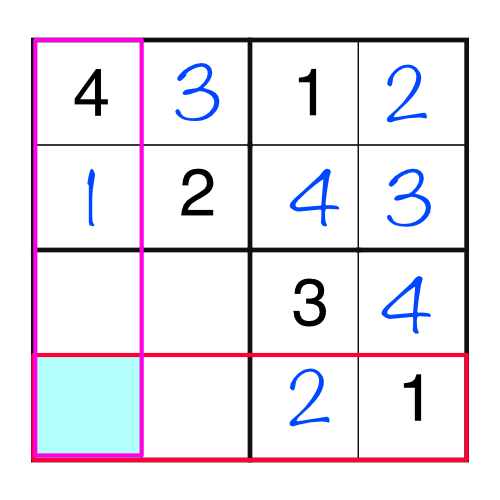
By looking at the intersection of the row and column highlighted, it’s obvious there’s only one number that can go in there. We can’t put a 4 or a 1, because they are already in the column, and we can’t put a 1 or a 2, because they are already in the row, so we’re only left with a 3.
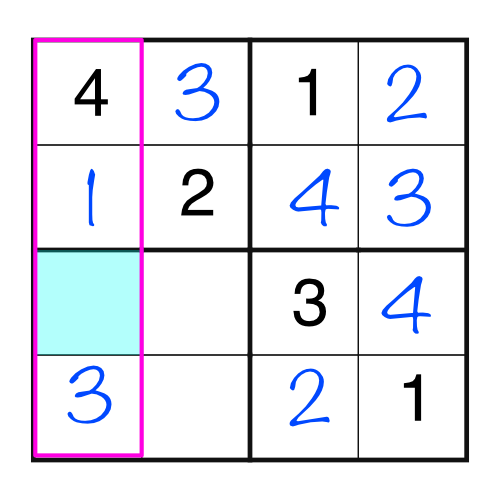
Once again, that simple logical leap has opened up the puzzle, and the remaining three cells are easy to fill in.

This introduction might be over-simplified, but it has been designed to give you the basis of logic required to solve sudoku puzzles.
Bigger puzzles, like those you’ll find in our books, can be solved with the same principles, although harder puzzles need some extra techniques. You’ll find lots of more advanced methods in the pages of this site.
In part two of this series we’ll look at regular sized sudoku, and introduces some helpful tricks you can use to solve puzzles up to intermediate level.
If you’d like to practice the very basics first though, we’ve put together a page of 4x4 puzzles below that you can print out.
4x4 Sudoku Practice — Solutions
Right click or long-tap and Download Linked File or click or tap to open in a new window then choose Print from your browser.