Suguru is a captivating number puzzle. At first glance it looks like a broken Sudoku grid. But whilst it shares some commonalities with its more well-known cousin, Suguru is a different kettle of fish altogether. If you’re new to Suguru, have a look at our tutorial here to get started.

One of the techniques that’s fundamental to solving harder Suguru puzzles is elimination by implication. We are going to look at some examples.

To start us off, we’re using a puzzle taken from A Year of Suguru (Easy to Intermediate) - the puzzle is from June 14 if you have the book and want to play along, and complete the rest of the puzzle yourself.

Here’s the grid as presented in the book:

Simple Implication

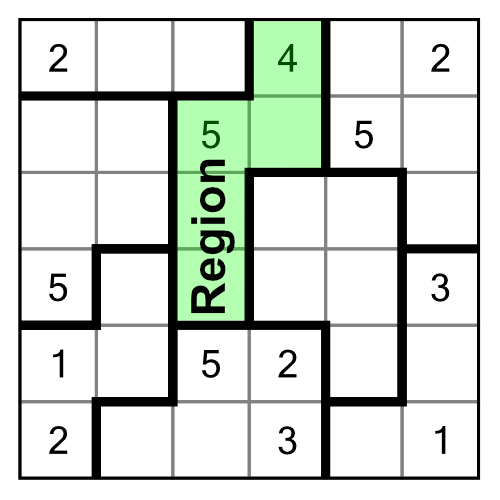
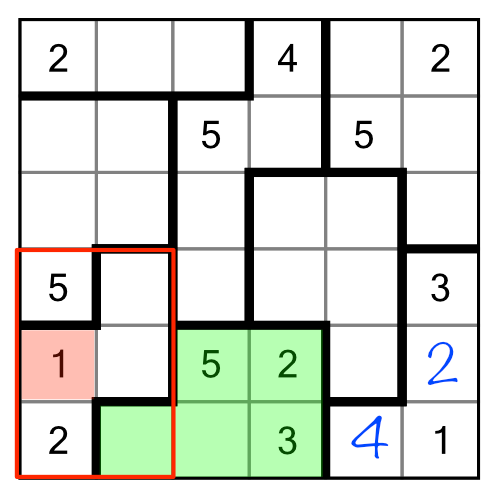
Let’s begin with an interesting example near the middle of the puzzle. I’ve highlighted two regions, green and red. The red region has no clue numbers in it at all, but we can still use it to solve the green cell with the ? inside:

We can solve this cell purely through implication. We know that the red region must contain the numbers 1, 2 and 3 (because it contains three cells). It doesn’t matter what order they appear in that region, they will all affect the highlighted green cell because they are all adjacent to it either vertically or diagonally. That means our green cell (the one with the ?) cannot contain a 1, a 2, or a 3. It also cannot contain a 4 because that already appears in the green region. Therefore the only number that can go there is a 5.

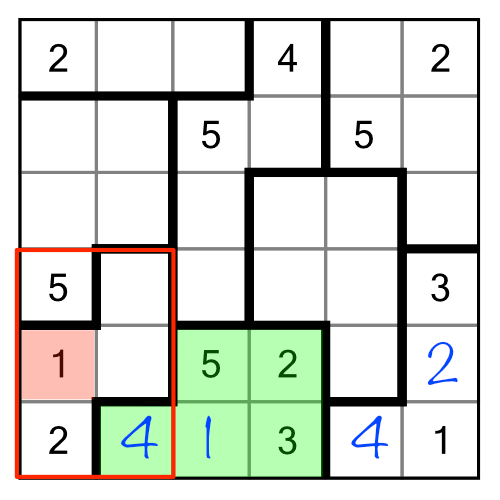
Even though the neighbouring region contained no clue numbers, its size and position made it useful. This was an example of simple implication. The implied contents of one region allowed us to directly solve a cell in a neighbouring one. But implication can go further.

Implication Chains

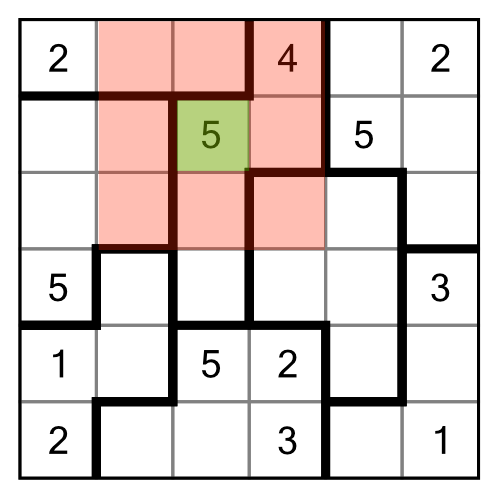
Let’s turn our attention to the bottom right of the grid. I’ve highlighted four regions that have some interesting interplay. 

We’ll begin with the green region. Given the presence of the 2 in the blue region above it, we know that the top cell of the green region cannot contain a number 2. Therefore the number 2 must go in one of the two bottom cells. This is a simple implication.

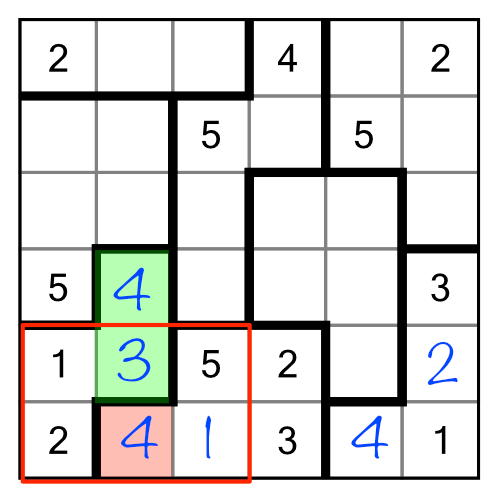
Because we now know that one of those two cells has to contain a 2, we can further imply that the left-most cell in the yellow region cannot be a 2. It doesn't matter which of the green cells is a 2, they both prevent the left-hand yellow cell from containing a 2. As there are only two cells in the yellow region, the left-hand cell must be a 1, which leaves the right-hand cell as a 2.

We’re not done yet. We can also infer, using the green region and the yellow one, combined with the blue one, that there’s only one place to put a 2 in the red region:

Here’s where it gets fun: the 2 we just filled in inside the red region now has a knock-on effect on the green region, telling us which of our two candidate cells must contain a 2 – the bottom one, it’s the only possibility.

Just by inferring that one of the bottom green cells must contain a 2, we’ve been able to fill in a neighbouring 2, which then allowed us to figure out another neighbouring 2, which in turn let us come back full circle and figure out which of the green cells must contain the 2! This is an implication chain at work, albeit a small one. They can get much, much longer.

Try One

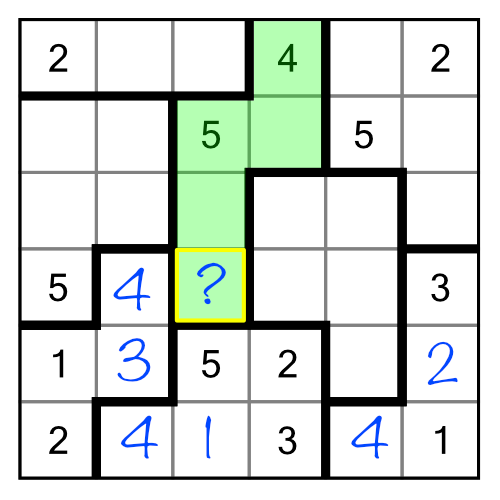
Here’s another example of an implication chain. This is the May 25 puzzle from the same book as above, if you want to play along. Here’s the empty grid, and I’ve highlighted three green cells that we can fill in through implication initiated from the red region. Can you work out how?

We’ll start with the 3 in the red region. This is a handy corner cell which eliminates three neighbours in the region just to the right. We can imply the position of the 3 in that region, narrowing it down to two possible cells, like this:

Even though we don’t know which cell contains the 3, we do know that either way, we can eliminate two cells in the region below. Furthermore, the 3 in the neighbouring yellow region knocks out two more cells, leaving only one place to put our 3:

That 3 then gives us the position of the 3 in the region to the right:

That in turn tells us where the 3 goes in the next region up:

Phew - after all that, even though we didn’t yet work out the position of the 3 in the first region, we could still use its implied position to fill in three other cells in the chain.

Summary

Implication chains are a powerful tool for solving more difficult Suguru puzzles. Even if a simple implication doesn’t let you fill in a cell, it’s worth trying to follow the chain because you never know where it will lead. It may even lead back in a circle, letting you fill in the original cell.

Chains can often come in handy for getting you moving if you get stuck, but they are just one tool in the toolkit for Suguru-solvers. Don’t get hung up only looking at chains, when often simple elimination will get you to a result more quickly.

If you want to try your hand at suguru but don’t know where to start, you’ve come to the right place. Assuming no prior knowledge of this captivating puzzle, we’re going to look at how the grid works, cover the simple rules, then dive in to the techniques we can use to solve it. Let’s get started, by looking at…

The Suguru Grid

Suguru grids do not have to be square. It’s possible to make puzzles of various shapes and sizes. Here at Puzzle Genius we are purists at heart, and we prefer the perfection of the square form. But we do publish puzzles of differing sizes — and of course — different levels. To start us off, here is an easy 1-star grid, six cells across by six down. It’s taken from our popular Pocket Suguru series:

Like a sudoku grid, we have some numbers filled in to start us off (clues). But that’s where the similarity ends. You’ll see there are no columns, rows, or blocks here. Instead we have regions. 

There is no fixed number of regions in a suguru grid, and the regions are not of fixed sizes. Indeed those two variables, along with the number of pre-filled clue cells, contribute to the difficulty of the puzzle.

Suguru Rules

Suguru’s rules are very simple. In fact there are only two:

• Every region must contain the digits from 1 to the number of cells within that region.
• Neighbouring cells cannot contain the same digit.

Looking back at our example grid, we note that the green shaded region has five cells, so it must contain all the digits from 1 to 5.

When we talk about neighbouring cells in suguru, we mean any cell that touches another horizontally, vertically, or diagonally. Here’s our example grid again:

If we consider the green cell 5, all the cells shaded red are its neighbours, so none of them can contain the number 5.

Just as with sudoku, we can always solve a suguru puzzle with logic. Guessing is not a strategy.

Solving Suguru Puzzles

Just like sudoku, some cells in a suguru puzzle are very easy to solve right off the bat with nothing more than a simple application of the rules.

Our puzzle has a an obvious place to begin. The region in the bottom right has four cells and is missing a 2 and a 4:

The presence of the 2 highlighted in red means we cannot put another 2 anywhere inside the red outline. That rules out one of our empty cells in the green region. Therefore the 2 has to go in the other one, in turn leaving only one place for the 4.

We can apply the same logic here:

Our green region is missing a 1 and a 4. The red highlighted 1 rules out the left-most free cell in our region, leaving only one place it can go. The 4 must therefore go in the other one.

We can quickly fill in another couple of cells the same way:

The red highlighted 4 makes them easy to work out.

Elimination

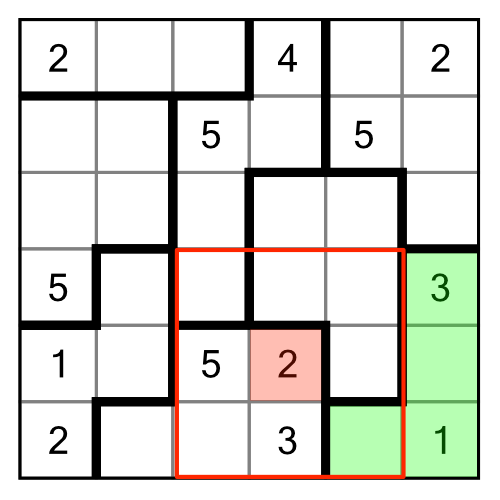
Once we’ve filled in the most obvious cells, we can move on to using an elimination strategy. Consider the region and cell highlighted:

At first glance this looks a little more complicated because now we have three cells within a region that we need to fill in. But actually we can apply the same logic to eliminate certain possibilities.

The red 3 and 2 prevent us from putting either of those numbers in our cell in question, which only leaves the 1.

Elimination By Implication

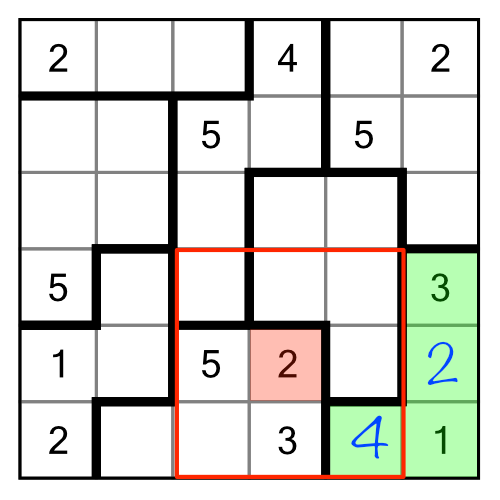
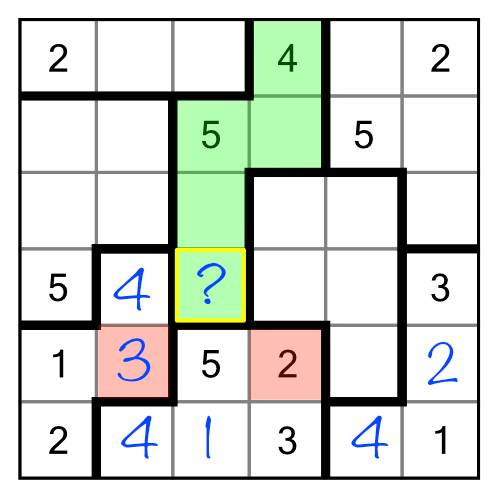
There’s another way we can use elimination, and it’s a bit more subtle. So far we’ve used pre-filled and solved cells to eliminate candidates. But in suguru we can also eliminate candidates based on implication. Consider the region with no numbers in it at all:

We know we need to find all the digits from 1 to 5 to fill this region. We can use the neighbouring (red) region to help us get started. The red region needs a 2 and a 3 in order to be completed. Given how our green region is partially surrounded by the red one, we can automatically eliminate 1, 2 and 3 as candidates for the cell with a “?” inside, and of course we can eliminate the 5 as well. Even if we didn’t already have the 1 and the 5 filled in inside the red region, we could still eliminate 1, 2, 3 and 5 based purely on implication. Putting any one of them into our “?” cell would make the red region impossible to solve! Therefore we can deduce that the only possible digit that can go there is 4.

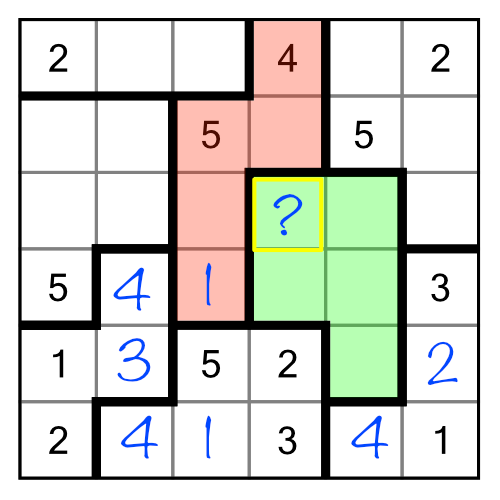
That’s a simple example of elimination by implication, but it’s a powerful technique that can be used to solve regions that at first glance appear to have no clues to go on. To see how powerful, here's an example from a different puzzle:

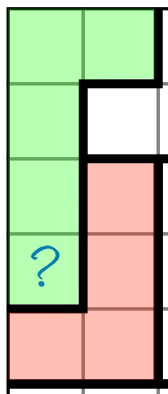
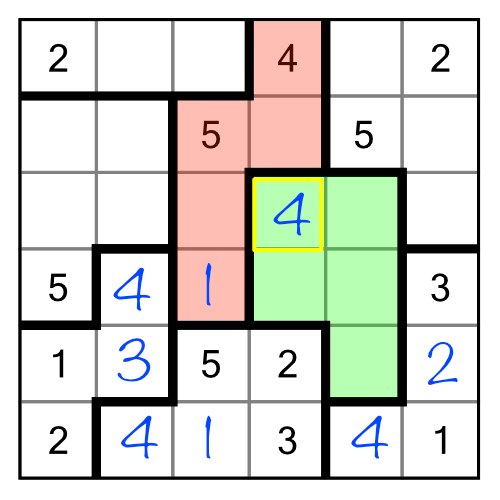
It looks like we have no clues at all to help us here, but of course that’s not true. There are certain things we do know. The green region has five cells, so requires the digits 1-5. The red region has four cells so needs 1-4. Elimination by implication tells us what the “?” cell contains. Given its position surrounded by the red region, it cannot contain a 1, 2, 3, or 4. If it did, it would be impossible to put any of those digits into the red region. Therefore it must contain a 5 - it’s the only option.

Solved

Looking back at our example puzzle, it can easily be solved now with simple elimination.

Note Taking

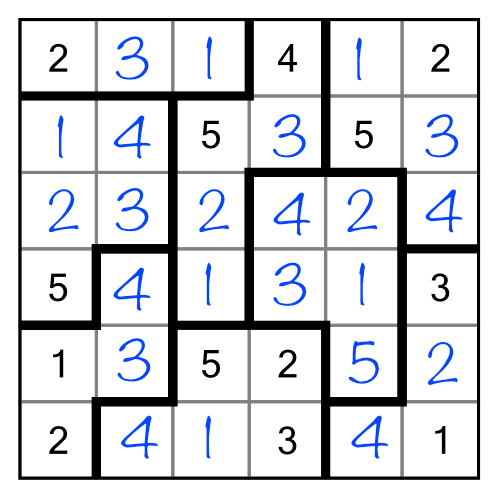
Just as with sudoku, writing in small numbers to show candidates for a cell can be a useful thing to do — especially on harder grids. It can ease cognitive load and show you opportunities that might not be obvious otherwise. Consider this puzzle:

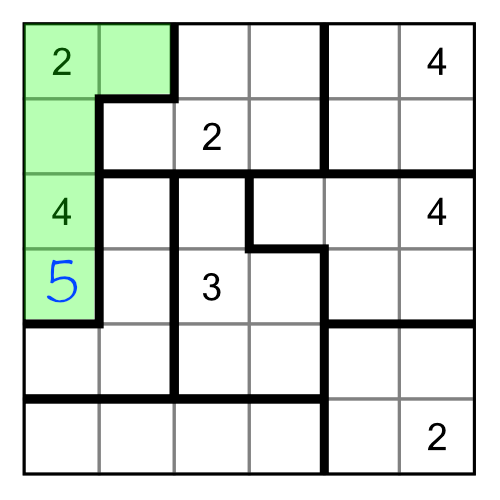
We’ve already solved the 5 in the green region based on elimination by implication. Where do we put the 1 and the 3 though? For now we don’t know, so we can write them in as little numbers:

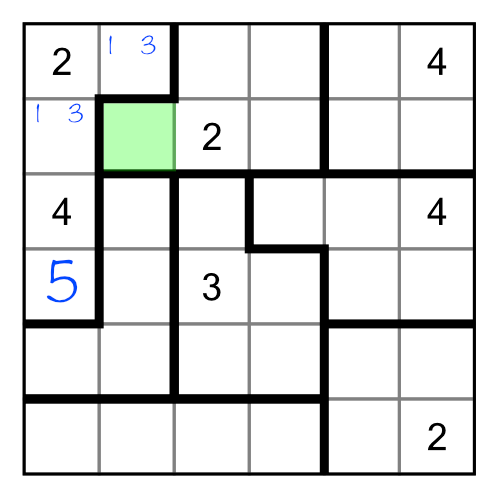
Now when we come to consider the green cell, we can immediately see that it cannot be a 1, 2, 3 or 4, so must be a 5. Yes, we could have worked this out without writing in the small numbers, but when working bigger puzzles with larger regions, taking notes like this can make it easier to spot answers as your notes will ripple out across the puzzle. When that happens, some combinations of notes will eliminate candidates in others, solving cells that then ripple back through your earlier notes.

Wrapping Up

Suguru is all about elimination. Elimination by implication can give you a quick ‘in’ to fill out some extra clue cells, helping you get started. Taking notes on harder puzzles will uncover hidden elimination opportunities.

If you find you get stuck in a puzzle, work through noting all possible candidates in the empty cells, and you will find pairs of candidates that, when combined, eliminate candidates from pairs of neighbours. 

To help you practice, we’ve put together a set of easy level suguru puzzles you can print out, along with the solutions in a separate PDF. You can download both below.

If you enjoy suguru and would like enough puzzles to keep you going for an entire year, then our A Year of Suguru books are for you. Large grids, and a daily rotation through five levels of difficulty mean you’ll have a fresh challenge every day of the year. Choose from Easy-Intermediate and Intermediate-Hard editions.