Sudoku is great fun whatever your age. But when it comes to younger people, this classic logic puzzle can be a fantastic educational tool. Like all the best learning tools, sudoku works well precisely because it is so much fun to play. Kids learn best when they are enjoying themselves, and sudoku has a lot to teach — and not just about numbers. Indeed sudoku, whilst traditionally using numbers, is not a math game. But it has a whole lot to teach.

At the bottom of this page you will find some free sudoku puzzles designed specifically for kids, that you can download and print out. But first, here are seven incredible benefits of using Sudoku as a learning tool.

1. It Reinforces Figure — And Letter — Recognition

Right from an early age, very simple kids sudoku puzzles are an excellent way to promote and reinforce the recognition of number forms. Even the simplest 4x4 puzzles are great at this.

By turning recognition into a game, the child is not only gently encouraged to differentiate between figures, but because they must find missing numbers, they will naturally create figures in their mind’s eye. This mental creation of numbers strongly reinforces the forms.

Of course, sudoku doesn’t just have to be played with numbers. Letters can be used instead, adding more learning opportunities. We’ve included both number and letter variants in our free downloadable kids sudoku puzzles at the bottom of the page.

2. It Teaches Problem Solving Skills

The aim of sudoku is to work out the missing numbers in a grid. The whole game is a puzzle that is crying out to be solved, so naturally playing it encourages and develops problem solving skills.

This can be done as gradually as necessary. A simple grid with a single missing number might seem to be so easy as to be pointless, but it’s like a gateway drug. When a child works out the missing figure, they experience a rush of excitement at having solved the problem; they are primed to solve more.

Building up the difficulty slowly and steadily maintains the challenge. The child is obliged to add a little more effort every time, and think up new ways of finding the answer — and being rewarded with the dopamine hit that comes with success.

As puzzles grow in size, complexity, or both, the child will have to find new ways to solve them. Thus what started as an easy game can soon become a fun and rewarding exercise in lateral thinking.

3. It Promotes Teamwork

Larger sudoku puzzles (typically full-size 9x9 and above) are a fantastic tool for encouraging working within a group. Puzzles can be split into racks and stacks, or columns, rows, and blocks, and each piece assigned to one or more children.

With a simple grid, the kids may initially solve the puzzle by working individually on their own portion. But ramp up the difficulty even just a little, and before long they will be obliged to co-operate and communicate to ensure their solutions do not ‘collide’ with those of the others in the group.

Take the difficulty up another notch, and the team will be encouraged to work together to come to a solution for the puzzle, pooling their techniques and knowledge.

For larger groups or older kids, try using 16x16 grids, or even better, Samurai Sudoku. The latter is a ‘multi-sudoku’ game with interlocking grids — perfect for splitting up and working on as a team.

4. It Encourages Attention to Detail

In a sudoku grid, a single mistake inevitably leads to disaster. Just one number out of place renders the entire puzzle unsolvable — not that it’s always immediately obvious!

It only takes a few failed solutions for most children to learn that they must check and double-check their answers before writing them in the grid, thus promoting careful attention to detail.

5. It Expands Memory

Logic is essential in solving sudoku, but so is memory. As they work through a grid, a child will be constantly putting numbers into very short-term memory, sometimes for just a few seconds at a time.

Sudoku is a great workout for the brain. Just as concentrated exercise can improve overall fitness, so working short-term memory improves overall memorisation and recall skills. Speaking of working out the brain…

6. It Improves Focus & Concentration

Sudoku demands a level of concentration that just isn’t necessary for most other kinds of puzzles. Simple math games, crosswords, word searches and so on, can all be done piecemeal by dipping in and out as and when. But to solve a sudoku grid effectively, it’s necessary to hold a lot of information in short term memory at once.

Losing focus, or lacking concentration, leads to mistakes or quite simply not being able to find a solution. Therefore the child is obliged to put all their attention into the job in hand. Studies show that concentration is like a muscle, and that repeated training leads to long-term improvement.

7. It Builds Confidence

If you’ve completed a sudoku puzzle then you know the rush of satisfaction that comes with putting that final number in the grid. One of the amazing things about sudoku is the range of difficulty that can be applied to a single concept. A child can learn the basics on a really easy 4x4 grid in a matter of minutes, yet be constantly challenged and stretched by the exact same set of rules right up to mind-bending super difficult 16x16 grids. Every win is an opportunity to boost their confidence and self-esteem, all whilst having lots of fun.

Download Free Sudoku Puzzles For Kids

Now you know why sudoku is such a great learning aid, as well as being a fun game, here are some grids that we have prepared especially for children.

We’ve included three grid sizes: 4x4, 6x6, and regular 9x9. There are eight 4x4 puzzles, and twelve of each of the larger sizes (which also include letter-based variants). Full solutions are of course also included.

The pages have been formatted so they will print on both American letter paper, as well as standard A4.

Looking For More Puzzles?

We’ve got you covered! We publish a brand new free puzzle every day. And of course, we have a large range of sudoku puzzle books of varying difficulty and size.

For kids sudoku, we highly recommend Amelia Baker’s range of books, which we collaborated on. You can find out more about those here. Amelia’s books include excellent tutorials written specifically for younger players, and lots of puzzles from 4x4 to 9x9.

Looking for a handy sudoku reference that you can print out and keep? Look no further! Our printable sudoku rules are just the ticket. Download the PDF below and print at home (or at work — we won’t tell your boss if you don’t!)

The PDF has been formatted to print nicely both on international A4 and US Letter paper.

Click or Tap Here For Printable Sudoku Rules

Sudoku For All Levels

Don’t forget that Puzzle Genius offers sudoku books for players of all levels. Be sure to check out the whole range here.

Part Three - Speeding Up

In part one of this tutorial we began by looking at the basics of sudoku, using smaller than normal puzzles. Part two took us through using racks and stacks to solve 1-star level full size puzzles. Now it’s time to ramp things up to the next level - literally.

We’re going to look at a 2-star grid and learn a couple of techniques that will help you solve puzzles faster, and prepare you for even higher-level puzzles along the way.

If you’ve arrived here without any knowledge of sudoku, I’d highly recommend going back and covering those earlier sections first - everything here will make a lot more sense that way.

Levelling Up

Here’s a 2-star puzzle, taken from our Pocket Sudoku — Classic range:

If you want to follow along yourself, you can download this grid to print out at home here.

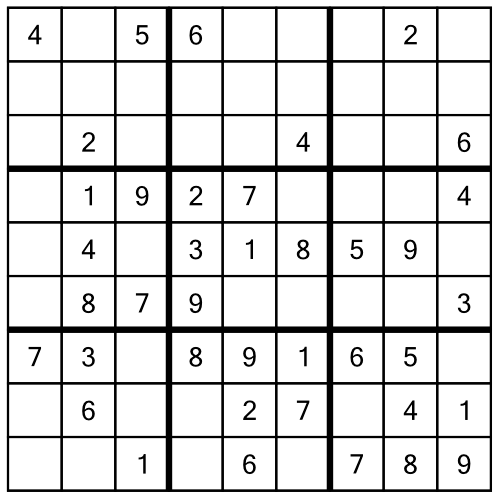
A quick glance at the puzzle tells us there aren’t any easy single free cells to fill in - every row, column, and block has at least two empty cells. So we begin by working the racks and stacks. This time I’m going to do the racks first, because why not? There’s no right or wrong way to attack a sudoku puzzle.

Working across the top rack, we can fill in a 2 and a 4. When we get to the 6, there are two possible cells it could go in:

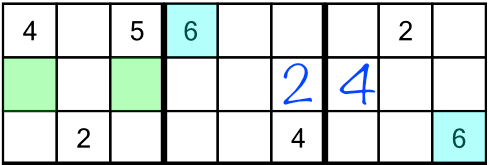
We could move on and look for the next number — it’s what we did back in part two of this tutorial in situations like this. But there’s a better way. Instead, we will write a tiny little number 6 in both the candidate cells, like this:

You’re probably wondering how this will help. Don’t worry, we’ll come on to that in a bit. First though, here’s some sudoku etiquette about how to write in little numbers. It’s best to always write them in the ‘correct’ place within a cell, because as we work through the puzzle we may end up putting more than one little number in a cell. Just jotting them down willy nilly will make our puzzle messy and hard to read. It’s better to have a system. To figure out where to write little numbers, just imagine the cell is filled with all the possible values, like this:

Sticking to this convention really makes working with the puzzle easier. By the way, it’s best to use pencil for solving sudoku puzzles because later you’ll want to erase the little numbers. It’s also good to have cells big enough to put several little numbers in without having to write microscopic digits. It’s why all Puzzle Genius sudoku books have generous sized grids - even our popular Pocket Sudoku range.

Back to our puzzle. There’s nothing more we can do with the top rack, so we move on to the middle one. Straight away we see that we have two candidate slots for the 1, so we can write in two little numbers:

Working through the rack we can fill in the 3, 4, 7 and 8. This is what the grid looks like so far:

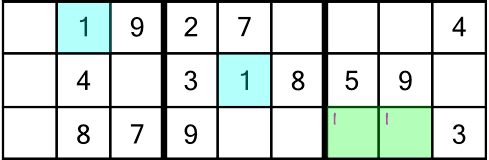
On to the third rack. The first opportunity we have to write anything in is the number 8. Again we have two candidate cells. We write in the little numbers, like this:

Now look what happens when we reach the number 9:

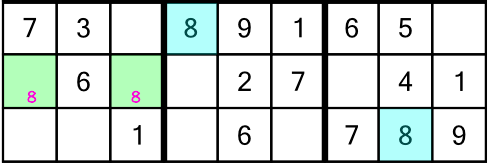
There’s a 9 in the middle block and top row (of the third rack), and there’s a 9 in the third block and bottom row. Logic tells us we have to put a 9 in the first block and middle row of the rack. There are two empty cells to consider, but one of them is out of bounds because there’s already a 9 in the column that cell is in. That leaves just one candidate cell, and it already has a little number 8 inside it. Remember, those little 8s are there to tell us one of the two cells must contain a number 8. When we write our 9 into the green cell (the only place it can go), we are ruling out the possibility of an 8 going in there:

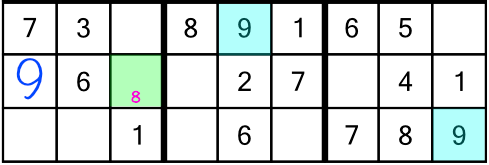
Now the only place left to put our 8 is the one remaining cell with a little 8 in it. Writing in the little numbers earlier meant we got to solve two cells in one go! 

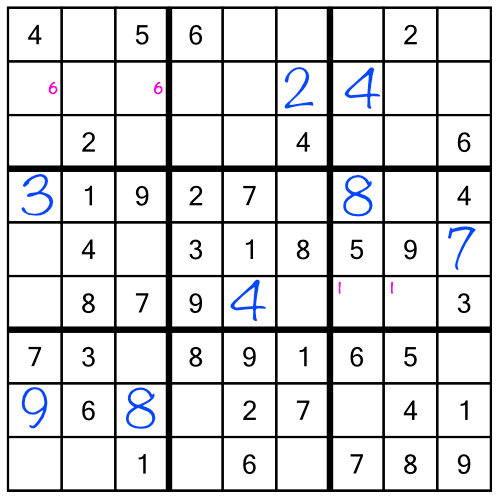
We would have found the 8 eventually, even without the little numbers. Our second tour through the racks — after we had worked through all the stacks — would have shown us where to put it. But doing it this way means we got to fill it in much earlier, saving us time and potentially making it easier to work through the stacks, because every completed cell makes the puzzle a little bit easier.

There are more benefits to using little numbers, and we’re going to cover one of those right now, as well as learning another technique that can speed up our sudoku solving powers!

Matching Pairs & Repercussions

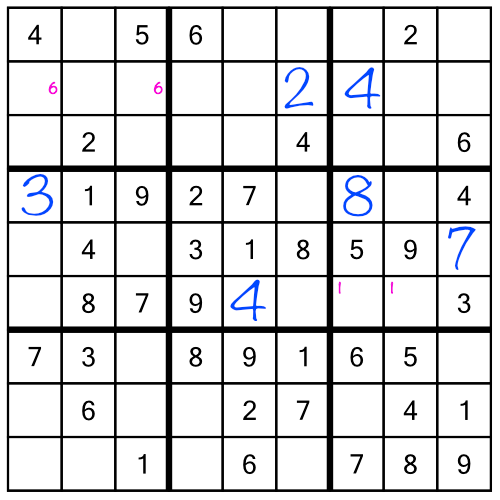
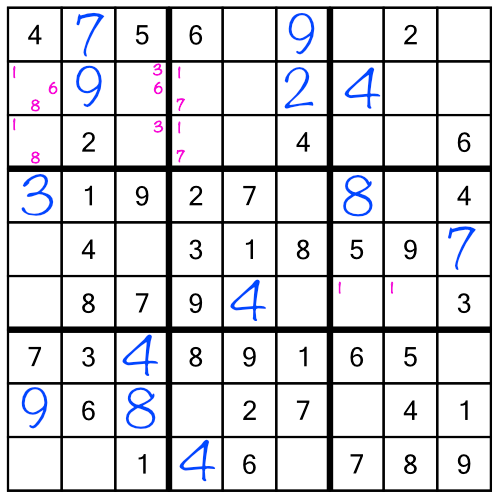
Let’s continue with our example puzzle. I’ve gone ahead and worked through the first stack, and the middle stack as far as the number 8. This is what the grid looks like so far:

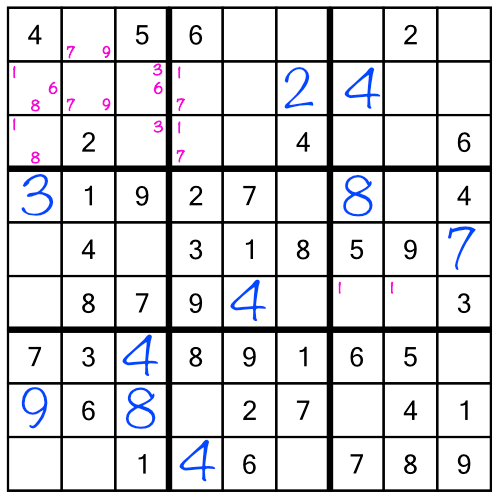
It’s starting to get a bit crowded - but don’t worry, all those little numbers are going to be a great help. Starting right now, when we add in the number 9 in the middle stack:

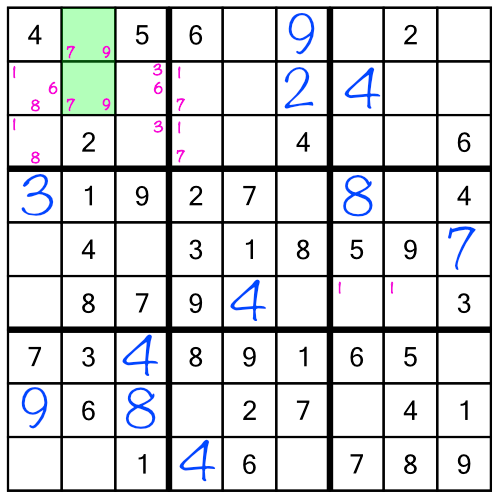
Looking back at the top left block, we notice the green cells both contain a little 7 and a little 9. When two cells in the same row, column, or block, contain two — and only two — little numbers, that tells us that they can only hold one of those two numbers. In other words one of those green cells must be a 7, and one must be a 9. There are no other numbers that could go there. And now that we’ve just filled in that 9 in the top row (middle stack), we’ve ruled out the possibility of the top green cell holding a 9!

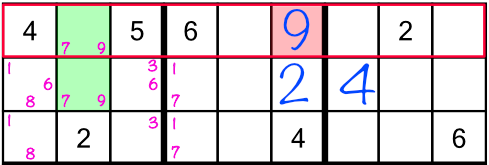
The repercussion of filling in the 9 in the top block of the middle stack is that now we know which green cell holds the 7 (the top one) and which holds the 9 (the bottom one):

Repercussions are an amazing way to solve puzzles more quickly. The technique is simple: every time we fill in a cell definitively (that is to say with a full size number, not a little number), we look at the puzzle to see if that number helps us solve any other cells. The repercussion of filling in the 9 in the middle stack was that we could solve the 7 and 9 in the left stack.

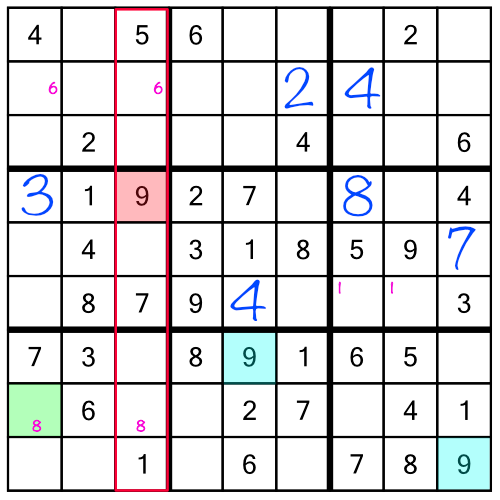
Before we move on working to the last stack, we can see if the 7 and 9 we just solved have any repercussions themselves

The 7s in the left stack are already all solved, and we don't have enough information to solve the 7s in the rack. But guess what? The new 9 means we can solve the third 9 in the top rack:

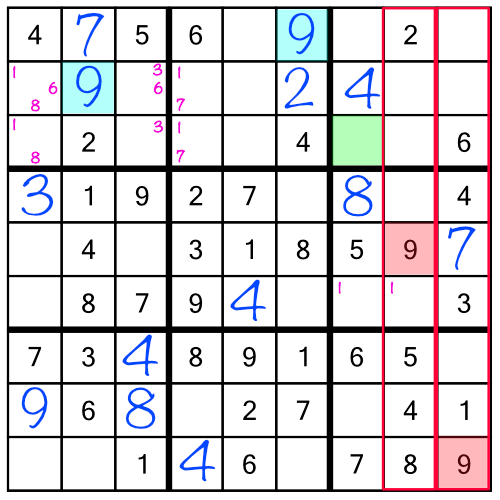
Now we've solved all the 9s in the puzzle. But that’s not the only repercussion. The 7 and 9 we added earlier have given us a single free cell in a column:

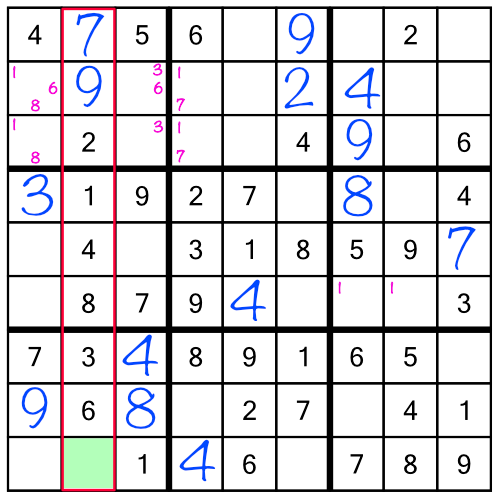
Filling it in with the number 5 gives us three more repercussions:

1. A single free cell in a block (green square, below).
2. A missing 5 in the left stack (yellow square).
3. A missing 5 in the bottom rack (purple square).

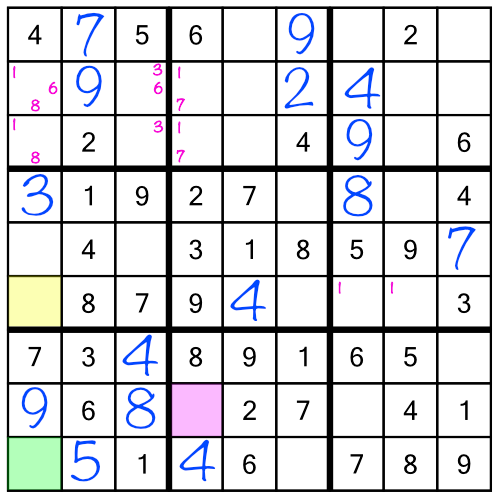
Filling in those numbers in turn gives new repercussions, and so on as the empty squares fall like dominoes. In fact, just by following the repercussions, we can solve the whole puzzle! We don’t even have to work through the final stack, and we certainly don’t need to work through the racks a second time.

Why not try and complete the rest of the puzzle yourself? When you are ready, you can download the solution here.

Wrapping Up

You now have enough techniques under your belt to solve 1 and 2-star puzzles, and with a bit of effort some harder ones too. There are plenty more techniques to discover though, and filling in those little numbers is key to making many of them work.

If you want to practice solving 2 star puzzles, we’ve put together some 2-star puzzles you can download and print out below, as well as the solutions to check your answers. And of course, we have a full range of high-quality sudoku books, including our popular A Year of Sudoku - with a new puzzle every day for a year.

Part Two - Racks and Stacks

In part one of this tutorial we began looking at sudoku from the first principles. If you’ve never tried sudoku before, we’d recommend going back and reading that page because it covers the basic foundations. 

Here in part two we are going to move on to full-sized 9x9 grids - the kind you’ll find in most books, including ours (though we do have some bigger versions for the more adventurous).

The Sudoku Grid

Here’s an empty 9x9 sudoku grid:

It’s just like the little 4x4 grid we looked at before, only bigger. The grid uses all the single-digit numbers from 1-9. Each row, column, and block must have each number 1-9 once, and only once.

Solving Sudoku Puzzles

Now let’s look at a real puzzle. This is an easy one - a one-star puzzle from our Pocket Sudoku - Classic range.

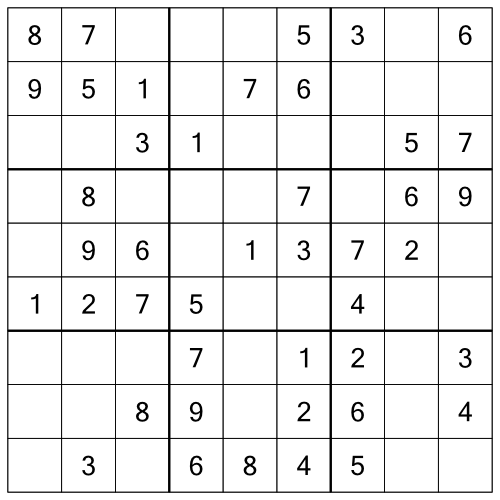
If you are new to sudoku, then at first glance a puzzle like this can look a bit intimidating. All those empty cells! What’s more, on closer inspection you might notice that unlike the little grids we looked at in part one, this one doesn’t have any rows, columns, or blocks with just a single empty cell.

Fear not. This really is an easy puzzle, and we’re going to deconstruct it to see why.

When we say deconstruct, we mean literally. We are going to break the puzzle apart and turn it into smaller bite-sized chunks that are much simpler to solve.

There are two ways we can break apart a sudoku grid. The first is by splitting it into three equal parts horizontally, along the thick lines, like this:

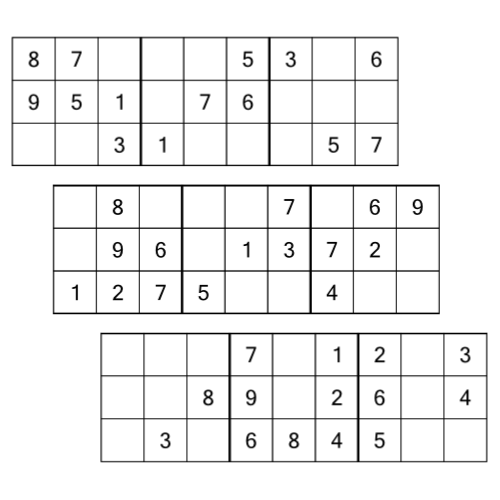
We call each of these horizontal sections a rack. As with everything in sudoku, different puzzle designers have different names for things. Rack is pretty common, and it’s what we stick with here at Puzzle Genius, but you might see racks referred to as ranks or even (confusingly) rows, in other places.

Looking back at the original grid above, you’ll see there are thicker lines running top to bottom as well. Splitting the grid vertically along those gives us three stacks, like this:

Again, different folks may have different names. We stick with stacks. 

Now obviously we aren’t going to physically cut out a sudoku puzzle and chop it up like this. But thinking of a grid as smaller racks and stacks makes it easy to tackle the puzzle because we’re only looking at three rows, columns, or blocks, at a time

One Rack At a Time

To see how using racks and stacks is helpful, let’s work through our example puzzle, starting with the top rack. 

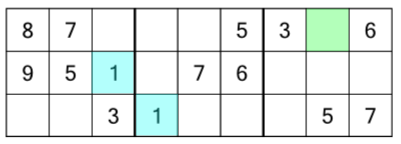
Step one of solving this grid is to look at where all the number 1s are in this first rack. There are two of them already filled in for us (highlighted here in blue). The first is in the first block and middle row. The second is in the second block and bottom row. We know every block and every row has to contain every number, once. So in this rack, logic tells us we need to put a number 1 somewhere in the third block, and somewhere in the top row. And guess what? There’s only one empty cell that falls in both the last block and top row. We have to put a 1 there. Like this:

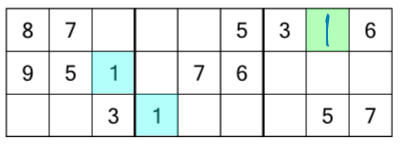
We can repeat this step, this time looking for number 2s. But there aren’t any number 2s in this rack, you say. And you’re right! No need to worry, we can move on and look for number 3s.

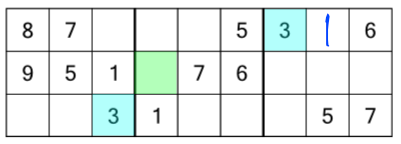
There’s a number 3 in the first block and bottom row, and one in the last block and top row. We must be missing a number 3 in the middle block and middle row. And again, there’s only one empty cell in that block and row (the green one), so we have to put a 3 in it, thus ensuring each row and block has a single number 3.

As you’ve surely figured out by now, we look for number 4s next, but there aren’t any. The number 5 already appears in each row and block, so we move on to the 6s. And here we have a bit of a problem:

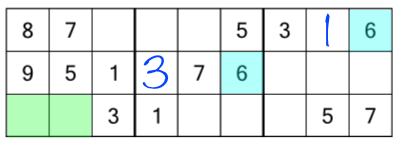
There are two 6s, and logic has narrowed down the possible homes for the third to two cells. Which one is correct? Right now we don’t know. We never guess in sudoku, because if we get it wrong we won’t know straight away and by the time we realise there’s an error in the grid, it will be far too late to work out where we made a mistake and we’ll have to start over. What then, are we to do? Simple: we carry on looking for the next numbers. We’ll come back to the 6s later. Right now we can check the 7s (they are all present already), and then the 8s:

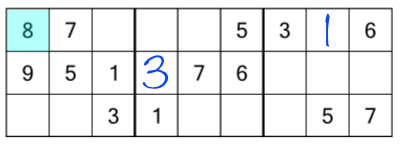
There’s only one 8, so we can’t draw any conclusions about where to put the others yet. The same is true of the 9. 

We’ve done all we can with this top rack (for now), so we can move on to the second rack and repeat the process.

There’s a 1 we can fill in in the top row of the rack, but the 2s are inconclusive, and we don’t have enough 3s, 4s or 5s to work those out yet. Once again, the 6s present us with a minor dilemma:

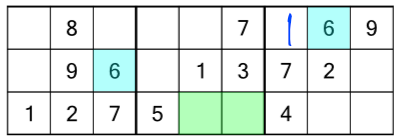
With a 6 in the middle row and first block, and one in the top row and last block, we know we have to add one somewhere to the bottom row and middle block. There are two empty cells there, but unlike the first rack, this time we can work out which is the correct place. How? By looking at the puzzle as a whole again:

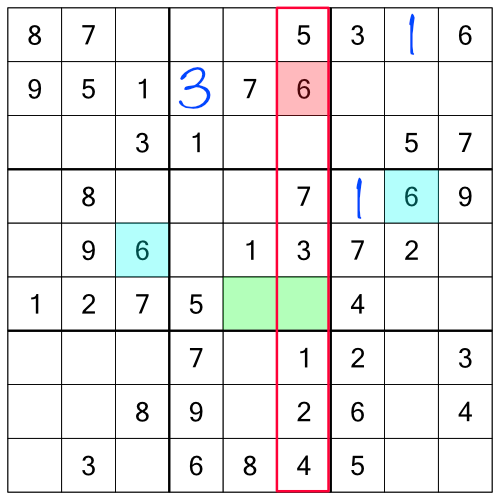
Looking at the entire grid allows us to consider not just the row and block, but also the column. And look - of the two cells we could consider for the 6, one of them is in a column that already contains a 6, so we know we can’t put it there. That only leaves one possible place for our missing 6:

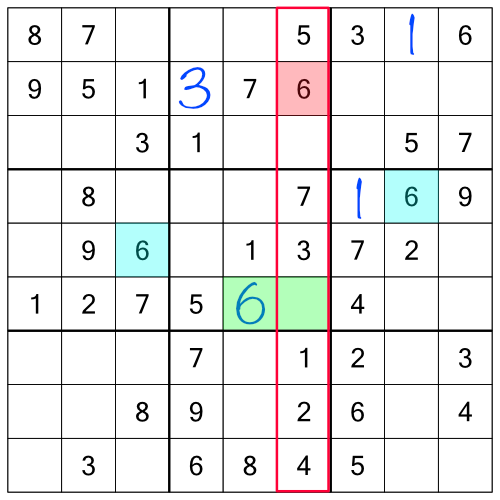
The 7s are all present and correct, and we only have one 8 so can’t do anything with that. The 9 in the middle row and the 9 in the top row tell us we need to put a 9 in the bottom row (middle block), and now we've only one free place to put it, so we can fill that in:

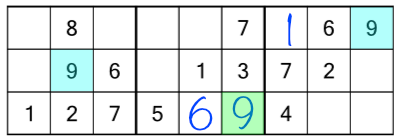
We do the whole process again for the bottom rack, where we find a missing 3 and 8.

This is what the grid looks like after working through the three racks:

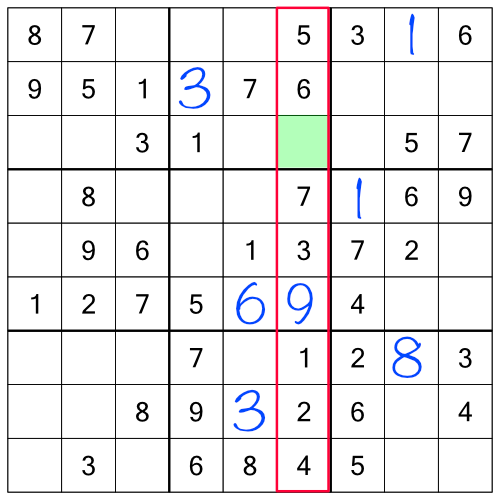
Working through the racks has allowed us to fill in enough empty cells that there’s now a column with just one number missing - a nice easy one to fill in. We also have an easy block to complete:

Here’s what the puzzle looks like so far:

Stacking Them High

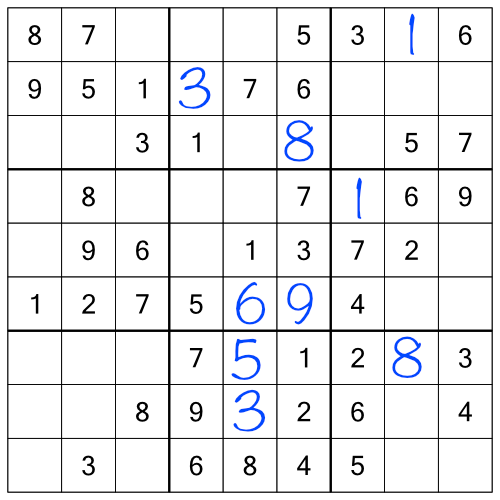
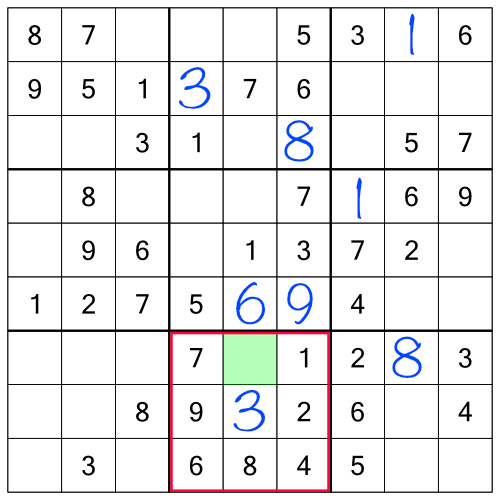
With the racks done, we can turn our attention to the stacks. The principle is exactly the same - take each stack in turn and work through the numbers to see what we can fill in. First up, the 1s in the left-most stack:

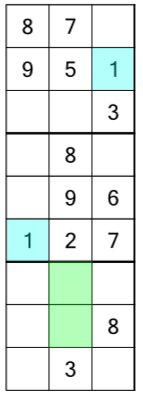
With a 1 in the top block and right column, and another in the middle block and left column, we know we have to find a place to put a 1 in the bottom block and middle column. There are two free cells there, so which do we go with? Once again, we can look at the whole grid to tell us:

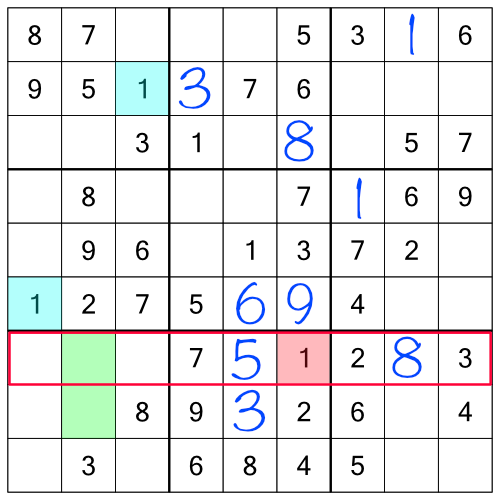
One of those rows already has a 1, so that only leaves one possible empty cell to put our missing 1.

After going through all the stacks using everything we’ve learned so far, our grid looks like this:

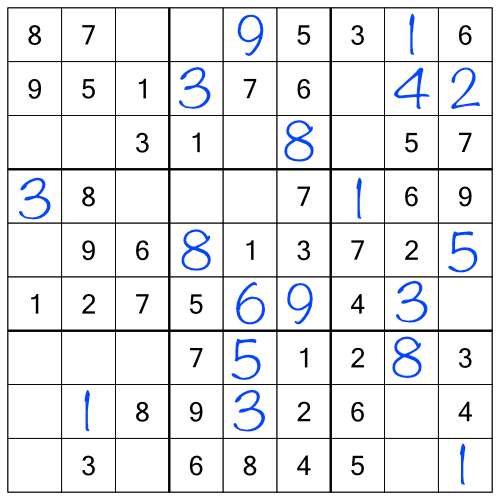
We’ve made some impressive progress, but obviously we’re not done yet. So how do we move forward? We could go back and go through the racks again. Having added in some extra numbers by working the stacks, we will almost certainly find that re-doing the racks will yield more answers. Indeed repeatedly working through racks and stacks might get us all the way to the end.

The Bigger Picture

Before we do that though, looking at the puzzle as a whole shows us there are some easy cells to fill in - single free cells within rows, columns, blocks, or a combination:

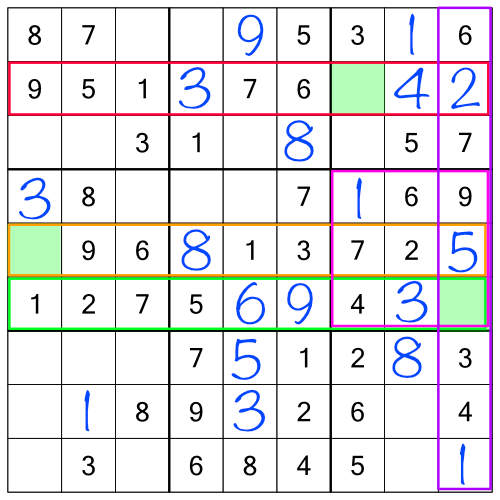
Filling all of those in makes the grid look like this:

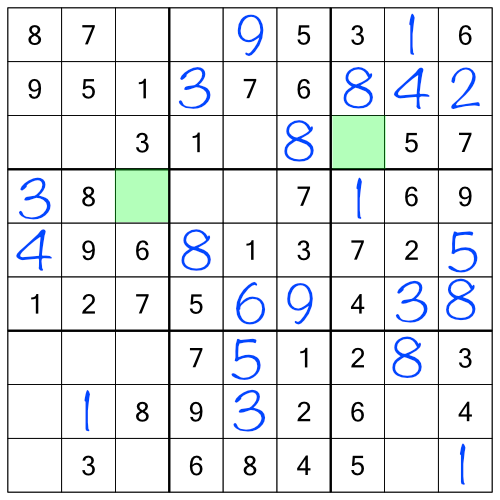
Now we’ve got even more single free cells to fill in. I said this was an easy puzzle! If we filling those, we get to this:

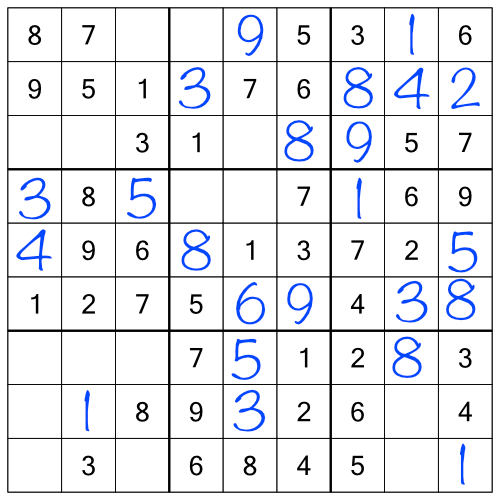
With no more single free cells, we can go back and work the ranks and stacks. At this late stage in the puzzle, we’ll find that often filling in a number as we work through the racks and stacks provides us with some easy single free cells we can fill in as well along the way. 

Following everything we’ve covered so far, by re-working the racks, stacks, and single free cells, we can quickly complete the puzzle.

The End?

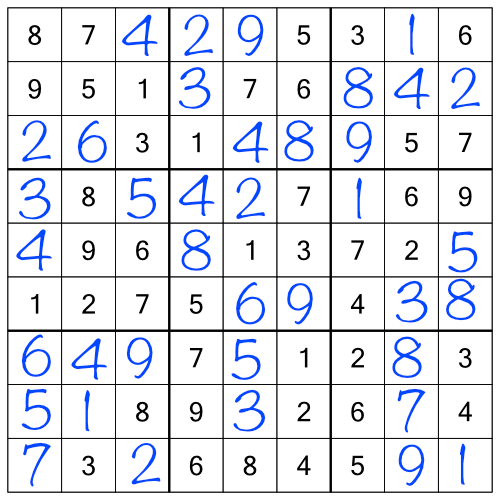
Congratulations! You now know enough sudoku to complete easy-level puzzles. Of course, there’s more to sudoku than just checking racks and stacks. Anything harder than easy-level grids will require some extra techniques.

To reach intermediate level, we are going to have to take things a little further. Part three of this series dives into a new technique that will take your sudoku-solving skills to a whole new level.

In the meantime, if you want to practice what you’ve learned so far, we’ve put together some easy puzzles you can download and print out, along with the solutions in a separate PDF.

And of course, we have loads and loads more puzzles in our books. Our Pocket Sudoku - Classic series is perfect for beginners. With five different levels of difficulty, you’ll find plenty of easy puzzles like the example we’ve just looked at. And as you learn more techniques, the higher levels will keep you busy too. All in a beautifully decorated, pocket-sized book you can slip into a pocket or bag and take anywhere.

Part One — Super-Simple Sudoku

If you’ve never played sudoku but want to get started, or if you’ve ever looked at a sudoku grid and found it intimidating or impenetrable, then you’ve come to the right place! This tutorial series assumes zero knowledge of the popular puzzle game. We’ll take you from scratch to being able to solve most puzzles up to intermediate level.

Sudoku is great fun, and is actually really easy to learn. It’s a good way to relax, to keep your mind sharp, and can be the perfect distraction from the difficult times we find ourselves in.

Contrary to popular belief, sudoku is not a mathematical puzzle. That it uses numbers is almost incidental. The numbers are just symbols, and in fact any kind of symbols can be used. Some kids sudoku grids use shapes or icons. Some sudoku puzzles use letters (these are usually called wordoku). Numbers are by far the most common symbol used in sudoku though, so that’s what we will stick with here.

The aim of the game is very straightforward: to find all the missing numbers in a partially filled grid of numbers.

To get started, we’re going to begin with a smaller than usual grid of numbers. It makes it easy to grasp the rules. What’s that, you say? What are the rules? Great question!

The Rules

The rules of sudoku are encapsulated in its name, which comes from the Japanese Sūji wa dokushin ni kagiru, which means the numbers must be single. In sudoku, each number in a grid can only appear once in each row, column, and block. 

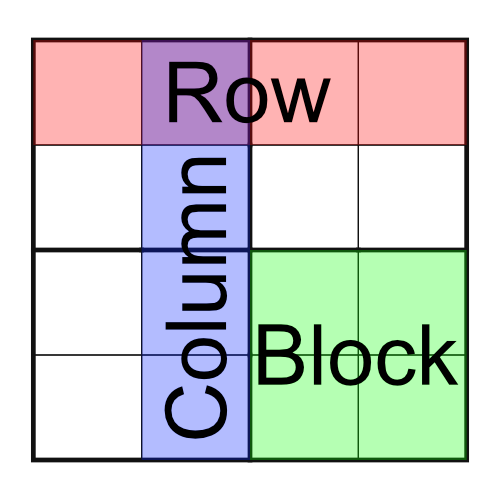
Before we go any further, let’s look at what a grid looks like, and explain some of that terminology.

The Sudoku Grid

Here's an empty sudoku grid. We call this a 4x4 grid because it’s four cells across and four down. Small grids like this are great for kids.

Note: If you have kids who you think would enjoy sudoku, we recommend Amelia Baker’s excellent Sudoku For Kids series. It starts with small grids like this and works up to full size ones, with fun tutorials along the way. It’s all wrapped up in a beautifully decorated book that kids will love.

The grid has four rows (each comprising four cells), four columns (of four cells), and four blocks - also made up of four cells. Some sudoku designers refers to blocks as boxes regions, or if they want to get really fancy, nonets. At Puzzle Genius we prefer to stick with calling them blocks because, well, they’re kind of blocky.

Here’s a 4x4 grid with some numbers filled in:

The aim of the game of sudoku is to fill in the empty cells with the missing numbers. We can always do this with logic - there’s no need to guess. In fact, guessing is very bad and should never be part of solving a sudoku puzzle. That’s because if we guess at the contents and get it wrong, we won’t necessarily know until we are much further into the puzzle. By the time we realise something is wrong, we won’t know where our mistake occurred and the only way forward would be to start over from the beginning.

Remember that sudoku comes from the Japanese for the numbers must be single? That means that:

• Each row in the grid must include all of the numbers 1,2,3 and 4.
• Each number is allowed only once in each row.
• Each column in the grid also has to contain all the numbers from 1 to 4.
• Each number can only show up once in each column.
• Every block in the grid also has to have every number from 1 to 4.
• And of course, each number can only show up once in each block.

Armed with the numbers already present, and these simple rules, we can solve the puzzle.

How To Solve Sudoku Puzzles

With a tiny grid like this, the logic to solve the puzzle is almost self-explanatory. But let’s lay it out there anyway, because making sure we understand the basics means we’ll have a good foundation for solving bigger, more complex grids.

The easiest place to start is with a part of the grid that’s already almost complete. Looking back at our example, which is super-simple, there are a few places we could begin. Let’s take the highlighted column which only has one number missing:

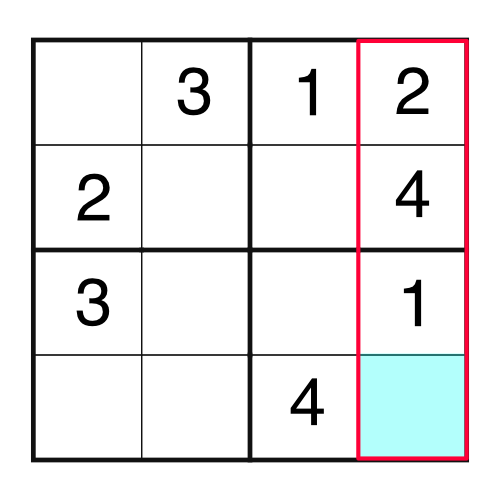
Given that column already has a 1, a 2, and a 4, the missing number is a 3. It’s the only number that can go in the blue square. We can write the 3 like this:

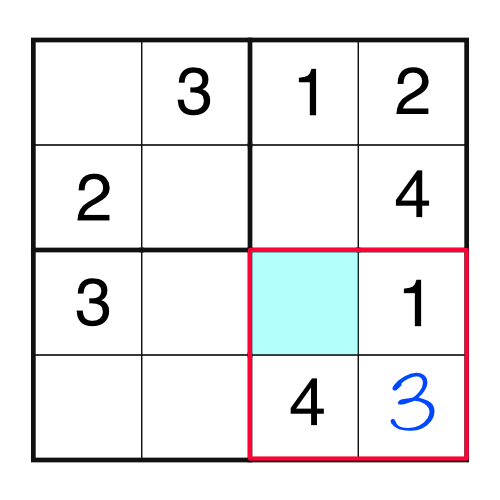
Now we have a block that’s only missing one number - the 2. Writing it in makes something interesting happen:

Look at that - there’s a block and a column that are both missing the same number. Fortunately they are missing the same number - the 3. If they were missing different numbers we would know we have a problem somewhere, because we’ve only got space to put one. Here’s what the grid looks like now:

 

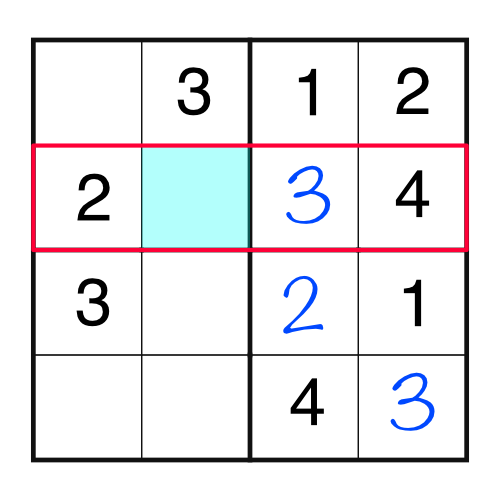
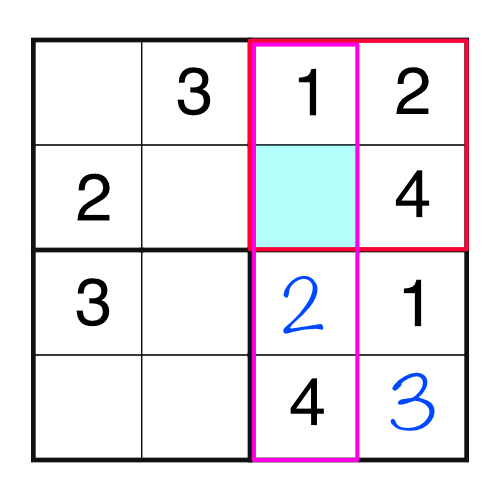
The next number is a 1:

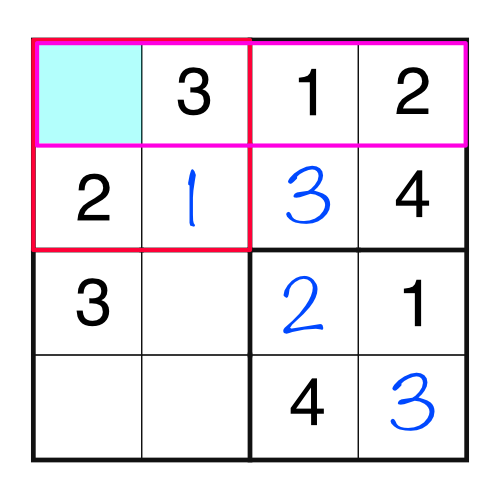
That gives us a block and row with the same empty cell, which has to be a 4.

It’s easy to keep filling in the single missing number each time until the whole grid is filled in. This is what the final solution looks like:

Many Roads

This example took one route to solving the puzzle, but it wasn’t the only route. There are no rules that say we had to start with the right-most column. It would have been just as easy to start with the top row, or the top-right block. In a puzzle this simple it’s possible to start in almost any cell. There’s no right or wrong way to proceed.

Checking The Result

The sudoku puzzle has been completed, but are we sure we got the result right? Checking it is easy - we just have to apply the rules of sudoku to each row, column, and block. Working top to bottom, we can read off each row to make sure that they all contain the numbers 1-4 once and only once. Then we can work left to right doing the same for the columns. Finally we can triple check everything is hunky-dory by verifying each of the blocks also contains each number once and only once.

Sales pitch alert! Checking 4x4 puzzles takes seconds. Checking regular sudokus, which are 9 cells by 9 cells, takes longer. That’s why every Puzzle Genius puzzle book contains complete solutions at the back, to make it much faster to check your results.

More Logic

The example we’ve just looked at was unusually easy. If every sudoku was that simple, the game would be very boring indeed. Let’s look at a more realistic puzzle, though we’ll stick with a 4x4 grid for this introductory tutorial.

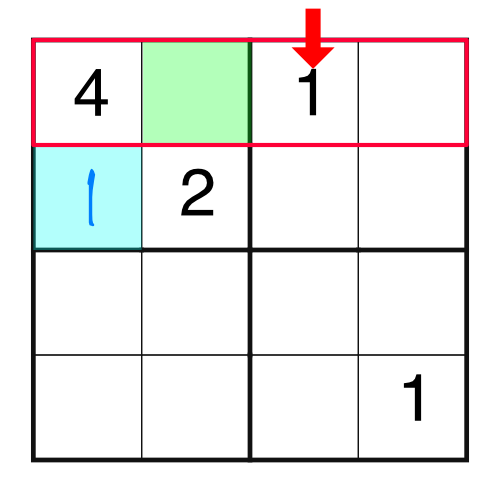
This time there are no rows, columns, or blocks that are missing only one number. The best we can do is the block on the top left, which is missing two.

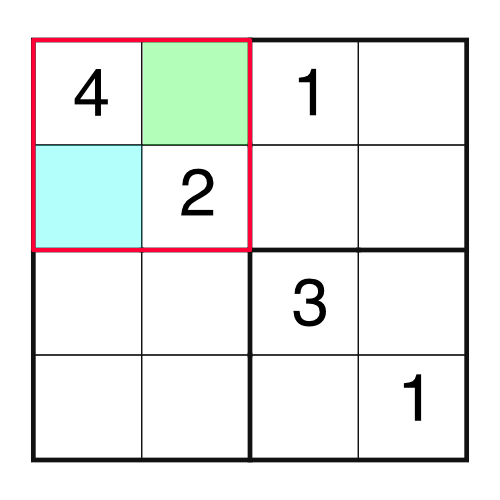
Logic is our friend. We have a 4 and a 2 in the block, which means we are missing a 1 and a 3. Which one goes in which empty cell? It’s easy enough to work out by considering other parts of the grid. For example, if we were to consider the top row, we would notice this:

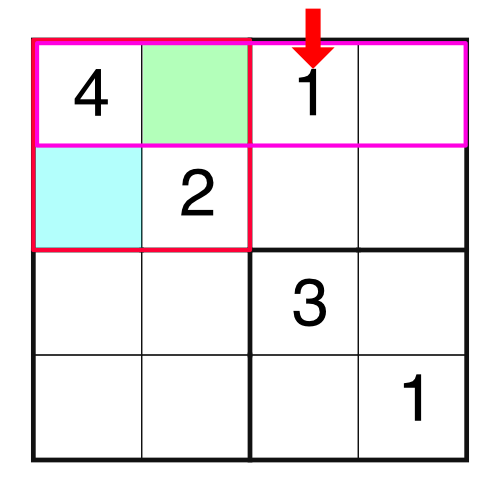
There is already a 1 in the top row, and we know we can’t put the same number into a row twice. That means we can’t put a 1 into the green square - we’d be breaking the rules. Therefore the only place the 1 can go in our highlighted block is the blue square.

Now that block is only missing a 3, so that’s what goes in the green square.

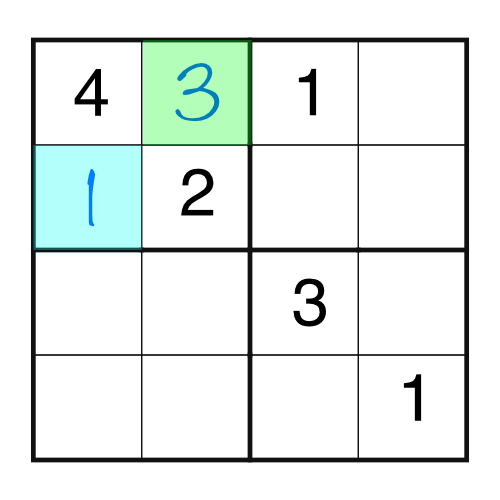
That little bit of login has opened up the puzzle. By filling in single missing cells we get to this stage.

At first glance, an entirely empty block might be difficult to solve. But it’s only a problem if we consider the block in isolation. Taking into account the rows and columns makes it a doddle. 

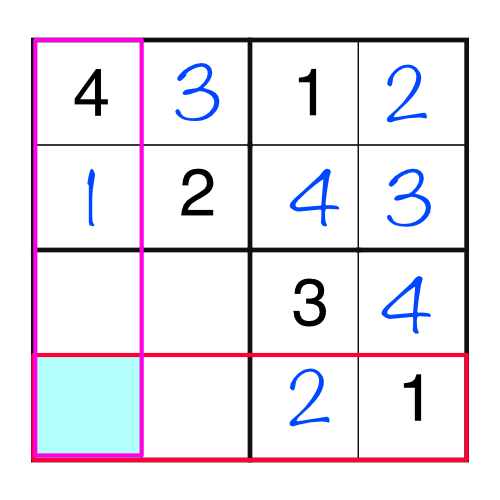
By looking at the intersection of the row and column highlighted, it’s obvious there’s only one number that can go in there. We can’t put a 4 or a 1, because they are already in the column, and we can’t put a 1 or a 2, because they are already in the row, so we’re only left with a 3.

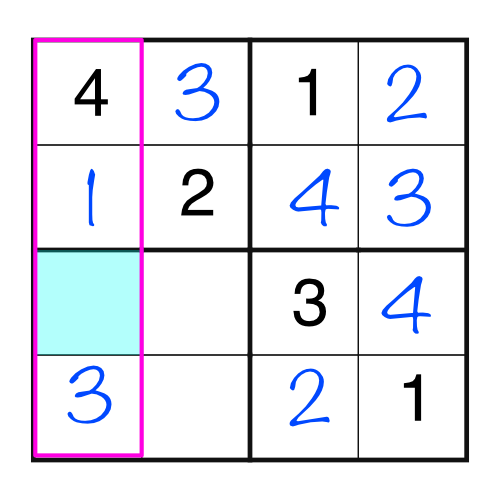
Once again, that simple logical leap has opened up the puzzle, and the remaining three cells are easy to fill in.

A Logical Foundation

This introduction might be over-simplified, but it has been designed to give you the basis of logic required to solve sudoku puzzles. 

Bigger puzzles, like those you’ll find in our books, can be solved with the same principles, although harder puzzles need some extra techniques. You’ll find lots of more advanced methods in the pages of this site.

Practice Puzzles

In part two of this series we’ll look at regular sized sudoku, and introduces some helpful tricks you can use to solve puzzles up to intermediate level. 

If you’d like to practice the very basics first though, we’ve put together a page of 4x4 puzzles below that you can print out.