Killer Sudoku From Scratch

If you’ve never played killer sudoku but want to get started, or if you’ve taken a look at a killer sudoku grid and wondered how on Earth you’re supposed to begin solving it, then you’ve come to the right place. 

Killer sudoku is like regular sudoku but with added mathematics. Unlike the classic game, there’s arithmetic involved. If that’s not your thing, killer sudoku probably isn’t for you!

A quick word of caution before we get started: killer sudoku is very much based on regular sudoku. You really need to know how to play the classic version before tackling this kind of puzzle. So if you’ve never solved a sudoku puzzle before, I would recommend reading through our Sudoku From Scratch guide, and doing some simple puzzles first (there are some free ones to download included in our guide).

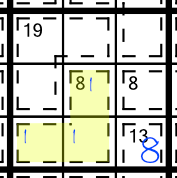
With that said, let’s dive in and look at a killer sudoku grid, and the rules that govern the puzzle. Here’s an easy grid to start us off — it’s a 1-star grid from our Pocket Killer Sudoku range.

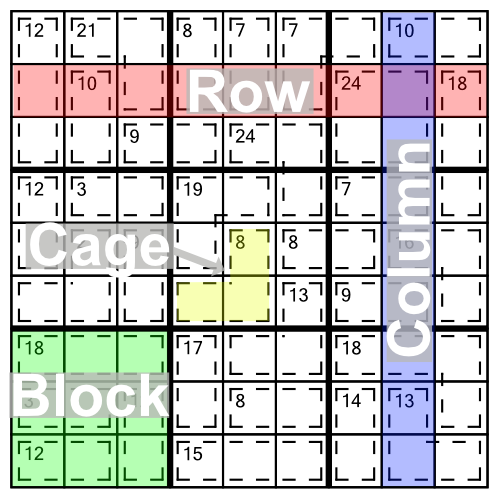
There are lots of things that are familiar about this grid if you are used to sudoku:

• It’s nine cells across by nine cells down.
• The grid can be split into nine rows and nine columns.
• There are nine blocks - sometimes called boxes, regions, or nonets. 
• Although we can’t see it here, the grid will ultimately be filled with the numbers 1-9.

There are also a couple of very obvious differences between a killer sudoku puzzle and the regular variety.

• Killer sudoku has an extra type of region, which we call a cage (highlighted above in yellow). Cages are delimited by dashed lines. They are not restricted to columns, rows, or blocks - they can cross those boundaries.
• None of the final digits are filled in. Instead we have a lot of little numbers to provide our starting clues.

The Rules

The first rule of killer sudoku is the same as sudoku:

• Every column, row, and block must contain the digits from 1 to 9 once, and only once.

To this we add a new rule:

• The sum of the digits within each cage must equal the clue number shown in that cage.

There’s the arithmetic; every killer sudoku puzzle involves a bit of adding up.

Looking back at our example grid above, we can see that the yellow cage has a little 8 written in the top cell. That means that the three numbers that go in that cage must add up to eight.

Whether you want to do your killer sudoku arithmatic in your head, or with the aid of a calculator, is up to you. But beware: any mistakes in adding up clue numbers will lead to errors that make the puzzle impossible to solve!

Solving Killer Sudoku

Solving killer sudoku puzzles requires a number of techniques. Some of those are the same as regular sudoku. Hidden and naked singles, single free cells, matching pairs and so on, all work exactly the same. But of course to use those we need to have some cells filled in, and when we begin a killer sudoku there aren’t any. So we can’t begin solving a killer sudoku puzzle the same way we would with a regular grid. We have to find another means of making headway. We need some specialist techniques, and that’s what we’re going to learn now.

Killer Sudoku Techniques

The 45 Rule

When we add up all the digits from 1 to 9, we get 45. We can therefore deduce that the sum of every row in a killer sudoku grid must be 45, that the sum of every column must be 45, and the sum of every block must also be 45. How does this help us solve a puzzle? Consider our example grid again:

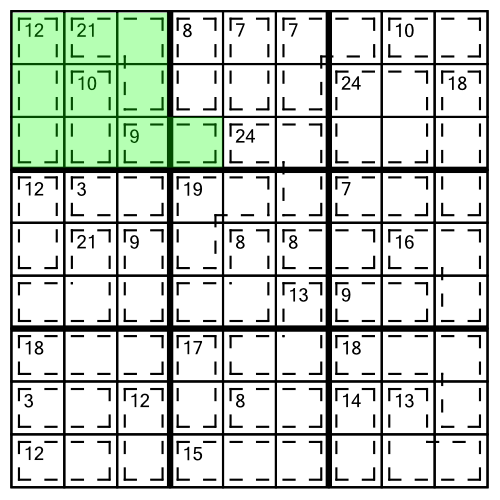
Looking at the top left block we notice that all but one of the cages are fully contained within it. The 9 cage spills over into the next block. We know that the sum of the block must be 45. We can add up the clue numbers (12+21+10+9) to get 52. That’s bigger than 45 - the maximum sum possible in a block. Therefore everything over and above 45 must fit into the single cell that spills out of the block. 52 minus 45 is 7, so that cell must contain a 7. Which in turn means the other cell in the cage has to be a 2:

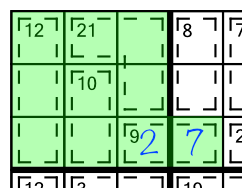
Naturally we can use the same technique on rows and columns as well as blocks. 

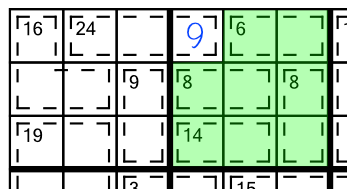
Sometimes cages don’t spill out out an area, they spill into one. Here’s an example from another 1-star grid:

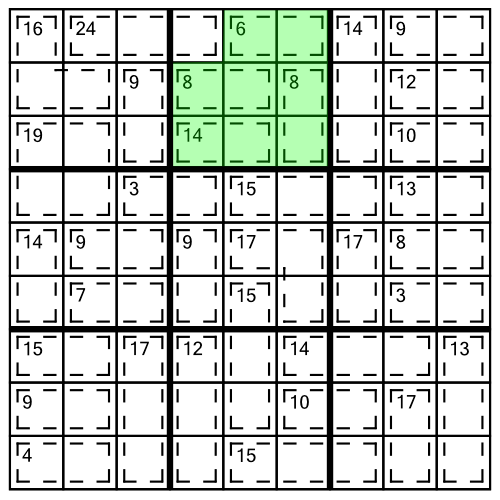
The principle is exactly the same. We add up the sum of the cages wholly contained within the block, to work out the value of the cell that has spilled into it.

6 + 8 + 8 + 14 = 36. We need all the cells in the block to add up to 45, so the cell that has spilled into it (the only one not shaded green), must contain a 9 (45 - 36 = 9):

Looking for places to apply this 45 rule is a good way to start a puzzle because it allows us to fill in some cells very quickly. Our example puzzles here are 1-star (easy) level. Harder puzzles won’t give up their secrets so easily. However, it’s worth keeping an eye out for places to apply this rule as you progress through a puzzle, because as cells get filled in, they can be used in the sum calculations, opening up more places to use this simple technique. 

Multiples of 45

We can take the 45-rule further by applying it to multiple columns, rows, or blocks simultaneously:

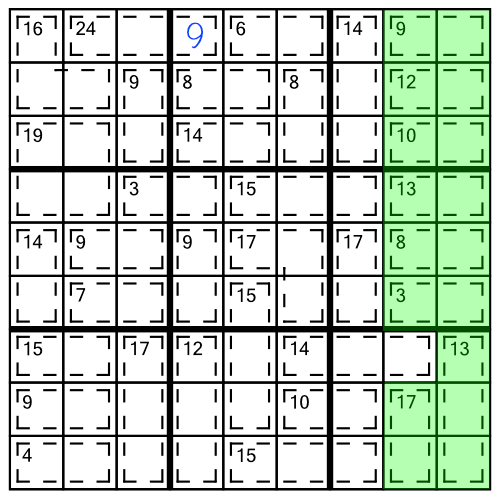
Neither of these columns alone are candidates for the 45 rule, but by combining them we find we have a single cell spilling inside. Working out its value is simple. We know the sum of the highlighted columns must be 90 (2 columns x 45). If we add up the clue numbers we get 85. Therefore the cell spilling into the columns must contain a 5, because 90 - 85 is 5.

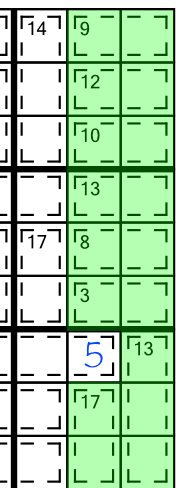
Here’s another example, this time combining three blocks together:

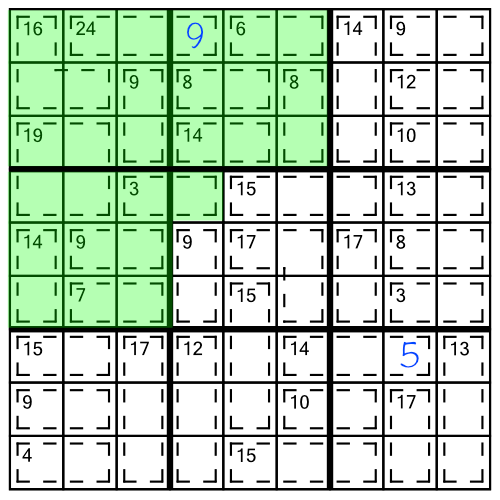
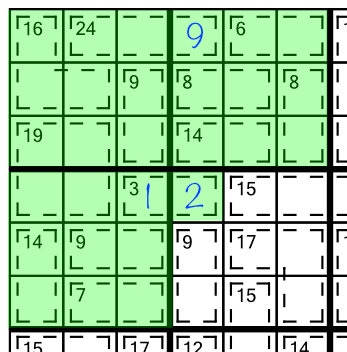
Adding all the clue numbers together gives us 137. As we have three blocks, we know the total should be 135 (3 x 45), so the extra 2 must go in the cell spilling out:

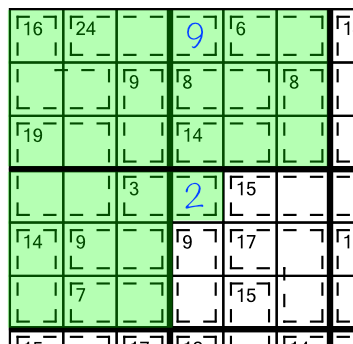
That in turn tells us we can put a 1 in the second and last remaining cell in that cage:

Limited Sum Combinations

For any given cage, there are only a limited number of digits that can legitimately add up to its clue number. This block contains a cage with an 3 in it, and it’s made of two cells. For brevity, we notate this as a 3(2) cage.

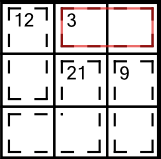
The only numbers that add up to 3 are 1+2. Therefore one of the cells must contain a 1 and the other must contain a 2. On its own this information doesn’t allow us to solve either cell definitively, but it narrows them down to two possible digits each, and we can write those in as little numbers, just like in sudoku:

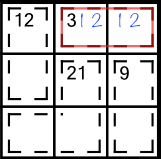
We know from sudoku that matching pairs like this are very useful. This one allows us to eliminate the numbers 1 and 2 from the rest of the row and and the rest of the block. 

Now let’s consider the example of an 8(2) cage (so that’s a two cell cage with an 8 written in it). Here are the possible combinations of numbers that could go in those cells:

• 1 and 7
• 2 and 6
• 3 and 5

Why not 4 and 4? Because no two cell cage could possibly contain the same digit twice — it would mean putting the same digit twice into a column or row. 

Knowing that each cell in an 8(2) cage could contain a 1, 2, 3, 5, 6 or 7 isn’t very useful. But other cages are much more restricted - as was the case with our 3(2) example earlier. To save you working out other combinations yourself, here are all the two-cell cages that can only contain two digits:

• 3(2) - 1 or 2
• 4(2) - 1 or 3
• 16(2) - 7 or 9
• 17(2) - 8 or 9

If you want to see the limited sum combinations for larger cages, take a look at our Killer Sudoku cheat sheet or use our Killer Sudoku calculator, which also lets you filter out combinations based on digits you need to include or exclude.

Required Digit Sums

There are certain sum combinations that always contain certain digits. For example, our yellow highlighted 8(3) cage right at the top of the page could comprise any of the following:

• 1 and 2 and 5
• 1 and 3 and 4

Knowing that any of the three cells in the cage could contain a 1, 2, 3, 4 or 5 is not very handy. But knowing that one of them must contain a 1 is much more useful. It allows us to write a little 1 into each of those three cells, thus eliminating it from the rest of the block. 

We’ve put the required digit sums into our cheat sheet too, to save you some more time. As with limited sum combinations, learning some of these by heart is a sure way to speed up your solving skills.

Combining & Reducing

We can push a puzzle a long way just by combining the techniques we have looked at so far, along with using what we already know about sudoku. Let’s work through a quick example. Consider the middle block of this right-hand stack:

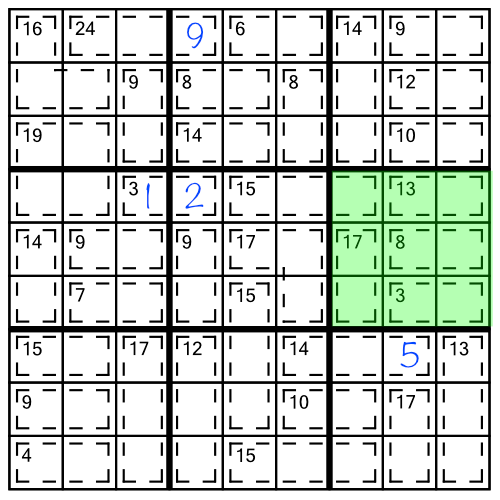
The first thing we can and should do, is work out the contents of the cell from the 15(3) cage that is spilling inside this block. Adding up the cages wholly contained in our block yields 41, so the intruding cage's cell must contain the missing 4 to bring us up to the requisite 45.

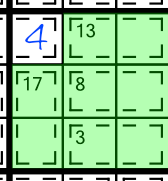
Next, based on what we know about limited sum combinations, we deduce that the 17(2) cage can only contain an 8 and a 9. And we can also work out that the 3(2) cage can only contain a 1 and a 2. Look what happens when we write in those little numbers:

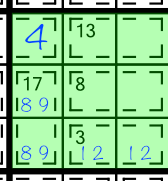
Knowing that this block already has the digits 1, 2, 4, 8 and 9 taken care of, reduces the possible candidates for the other cells. So whereas an 8(2) cage could normally take candidates 1,2,3,5,6 and 7, here we can reduce that list to 3,5,6 and 7. And in fact if we zoom out and look at the stack again, we notice that there’s already a 5 in the middle column, so we can reduce the options even further in half of the cage.

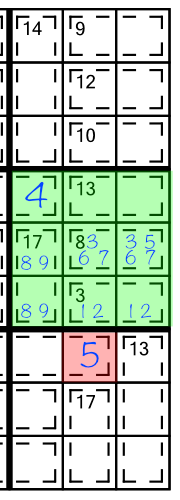
The same logic applies to the 13(2) cage. Normally it could hold a 4,5,6,7,8, or 9. Given what we know must already be in the 17(2) and 3(2) cages, and the cell that’s already filled in, we can reduce those candidates to 5,6, and 7. And again, the 5 already in the column reduces the options further in the first cell in that cage:

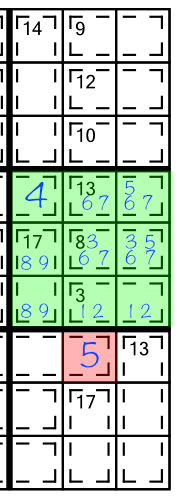
Working across the puzzle in this way, combined with regular sudoku techniques, is enough to solve easy-intermediate puzzles like the examples presented here.

Wrapping Up

The key to solving easy killer sudoku puzzles is to use all the tools we’ve covered, to eliminate possible candidates. Often you will find that you can reduce and reduce the possibilities within a cage so far that you solve one cell in the cage. That in turn reduces the possible candidates for other cells within the same cage, and so on.

Remember to always look at the repercussions of each cell you solve — in killer sudoku even more so than in regular sudoku, solving a single cell can have huge repercussions that ripple out across the whole puzzle.

What starts off as a seemingly impenetrable grid, can very quickly evolve into something that becomes easy to solve as you combine the killer sudoku sum clues with regular sudoku techniques.

If you want to practice solving 1-star puzzles, we’ve put together a set you can download and print out below, as well as the solutions to check your answers. And of course, we have a full range of high-quality killer sudoku books, including our popular A Year of Killer Sudoku - with a new puzzle every day for a year.