Hitori

Hitori is a logic puzzle that, like Sudoku, uses numbers as symbols but does not involve arithmetic.

In a hurry? Jump to: Rules / Tips / Example / Download Free Puzzles / Hitori Books

The objective is to cross out certain numbers such that each column and row contains no more than one of any given number.

Here’s what a small, simple Hitori puzzle looks like:

Rules of Hitori

Your aim is to cross out, or shade, certain cells according to the following rules:

No digit can appear more than once in any row or column.
No two shaded (crossed out) cells can touch horizontally or vertically.
All unshaded (uncrossed) cells must form a single contiguous group. In other words, it should be possible to trace an unbroken route from any unshaded cell to any other unshaded cell.

Here’s what our earlier small example puzzle looks like, once completed:

The solution to a small Hitori example puzzle

Solving Hitori Puzzles

Hitori puzzles are solved with a combination of elimination and logical deduction. When solving, it helps if we remember we are not only looking for cells that we know must be shaded, but that we can also determine certain cells that must be left unshaded. These can be just as useful to discover as we work our way through the board.

Here are some tips for solving. Below, we’ll put them into practice and work through a complete puzzle from start to finish.

Begin with easy wins, looking for simple patterns that indicate cells that must be left unshaded. As you find these cells, it helps to circle the digit within.
When you circle a digit, you can then shade any duplicates of that digit within the same column and row because they cannot be allowed to remain.
When you shade a cell, you can circle any digits in cells that are above, below, and to the left and right of it (because shaded cells cannot touch orthogonally).
Here are some patterns you can look for to get an easy start:
- Three digits the same in a row (for example, a row contains 7,5,5,5,3,6). In these cases, the centre digit of the three cannot be shaded, but both outer digits must be. This is a simple logical deduction; shading the centre digit would render it impossible to shade either of the other duplicates.
- 2+1 of the same number in the same row or column (for example, a row contains 6,5,5,1,4,5). The single duplicate digit must be shaded (the end ‘5’ in this example). Again, it’s a simple logical deduction, as it would be impossible to shade the adjacent matching digits, that’s against the rules. One of that pair must remain.
- XYX pattern. That is to say, two digits the same with a different digit between them (for example, a row contains 1,3,4,3,5,6 – the 3,4,3 form an XYX pattern). In this pattern, the middle digit must be kept, so can be circled. This is a logical deduction because we know we’ll have to shade at least one of the two digits either side of it.
As you shade and circle digits, remember to look along both the row and column they are in to see if there are any knock-on effects. Often, just determining the status of a single digit can have an effect that ripples out all the way across the board.

Interestingly, contrary to puzzles like Sudoku, you can’t tell you’ve finished a Hidato puzzle simply by filling in a final missing digit. You have to work out when you’re done by constantly checking if there are any remaining duplicate digits. So it’s always worth double-checking before you declare your puzzle complete and check your result!

Worked Example

Now that we know how to attack Hitori puzzles, let’s work through an example from start to finish.

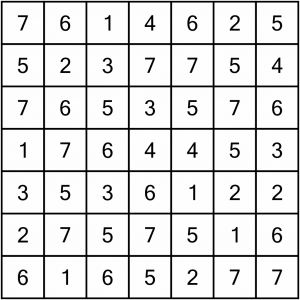
This is the puzzle we are going to solve. It’s a Level 1 puzzle; 7x7, easy to solve but sufficient to demonstrate the common techniques we use.

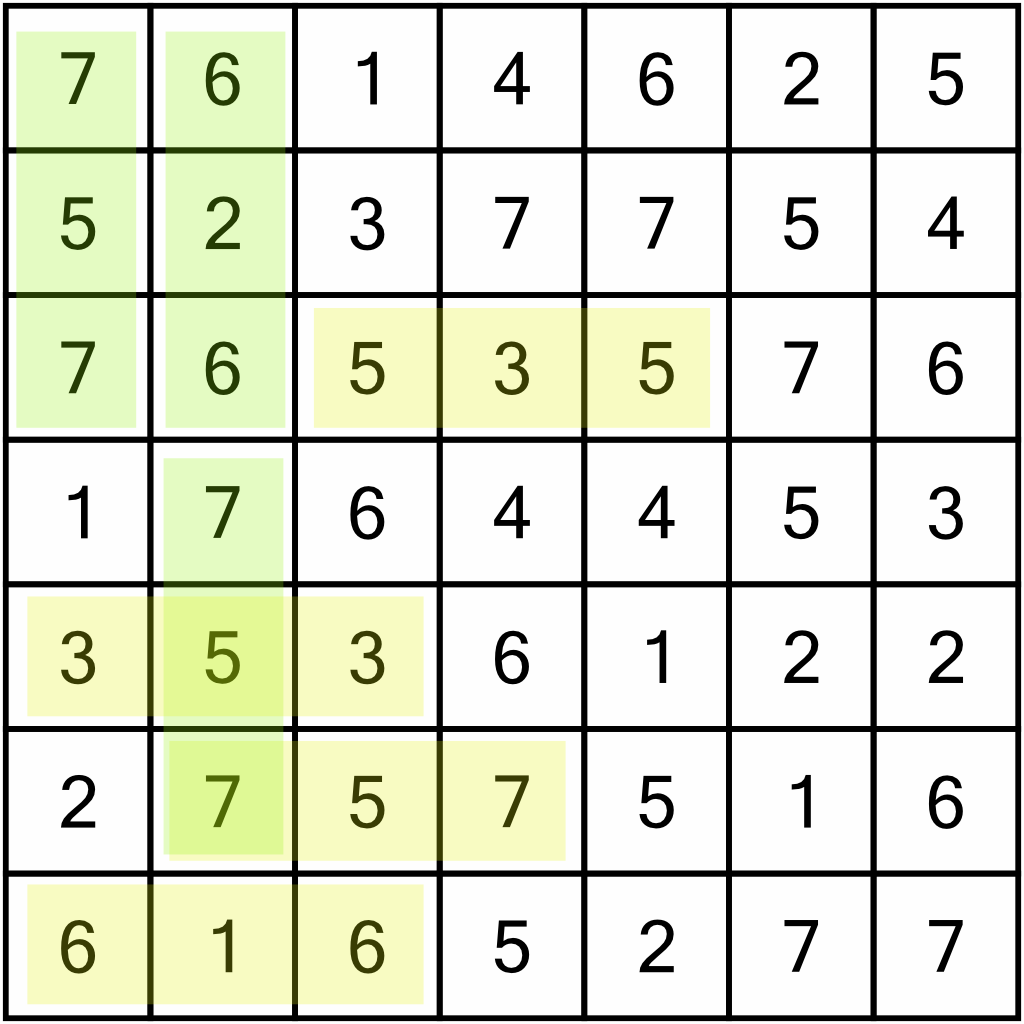
We’ll begin by looking for the easy patterns. There aren’t any ‘3 in a row’ patterns here, and neither are there any “2+1” patterns. There are quite a few “XYX”s though, which are shown here in yellow for rows and green for columns. We know that in each of these cases, we can circle the middle digit – it must be kept, because we know we’ll have to eliminate (shade) at least one digit immediately adjacent to it. We don’t know which will be shaded (and indeed it could be both), but it doesn’t matter, at least one will be and as we cannot have two shaded cells next to each other, the middle cell can’t be shaded so must be circled.

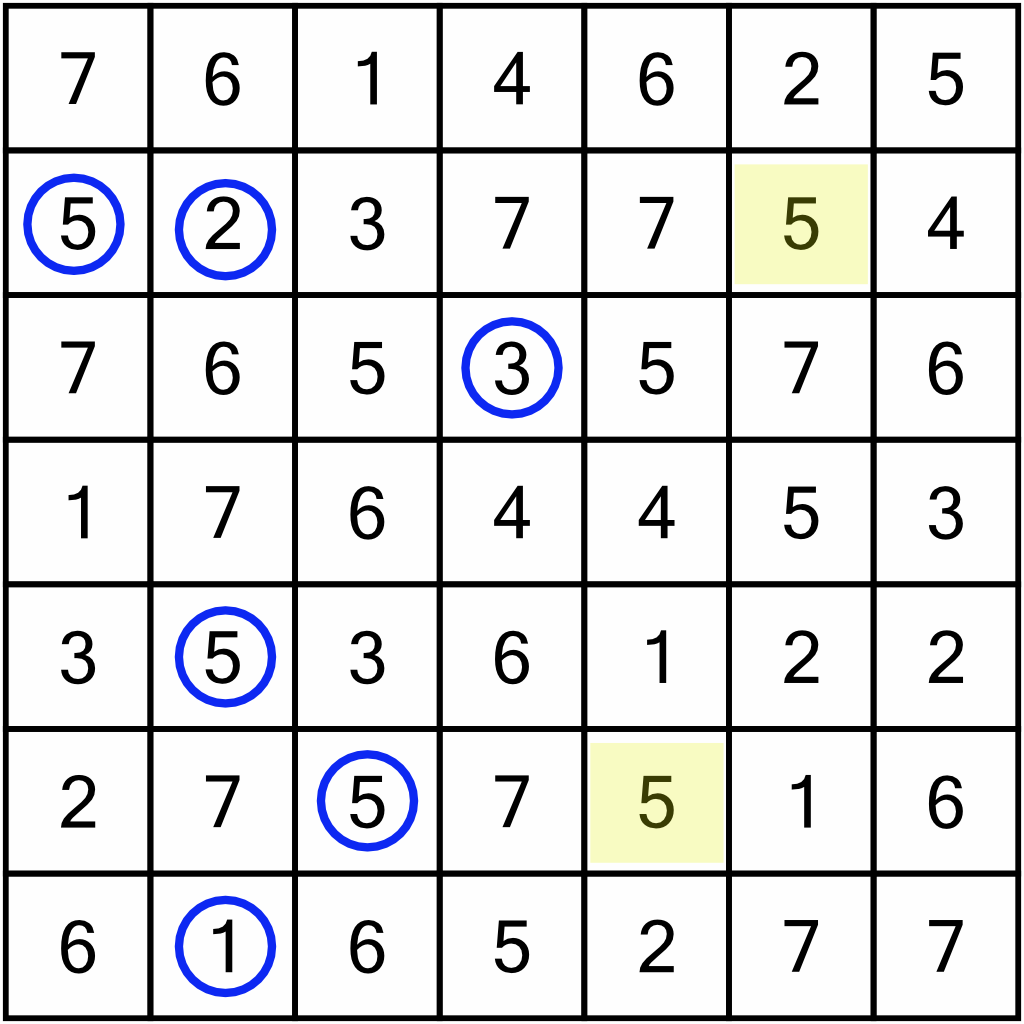
Now we can look along each row with circled digits, and see if there are duplicates of those digits. If there are, they can be eliminated. In row 2 we are looking for any other 5s and 2s. There is a 5, so we will be able to eliminate it.
Row 6 also has a duplicate 5 that we can take out.

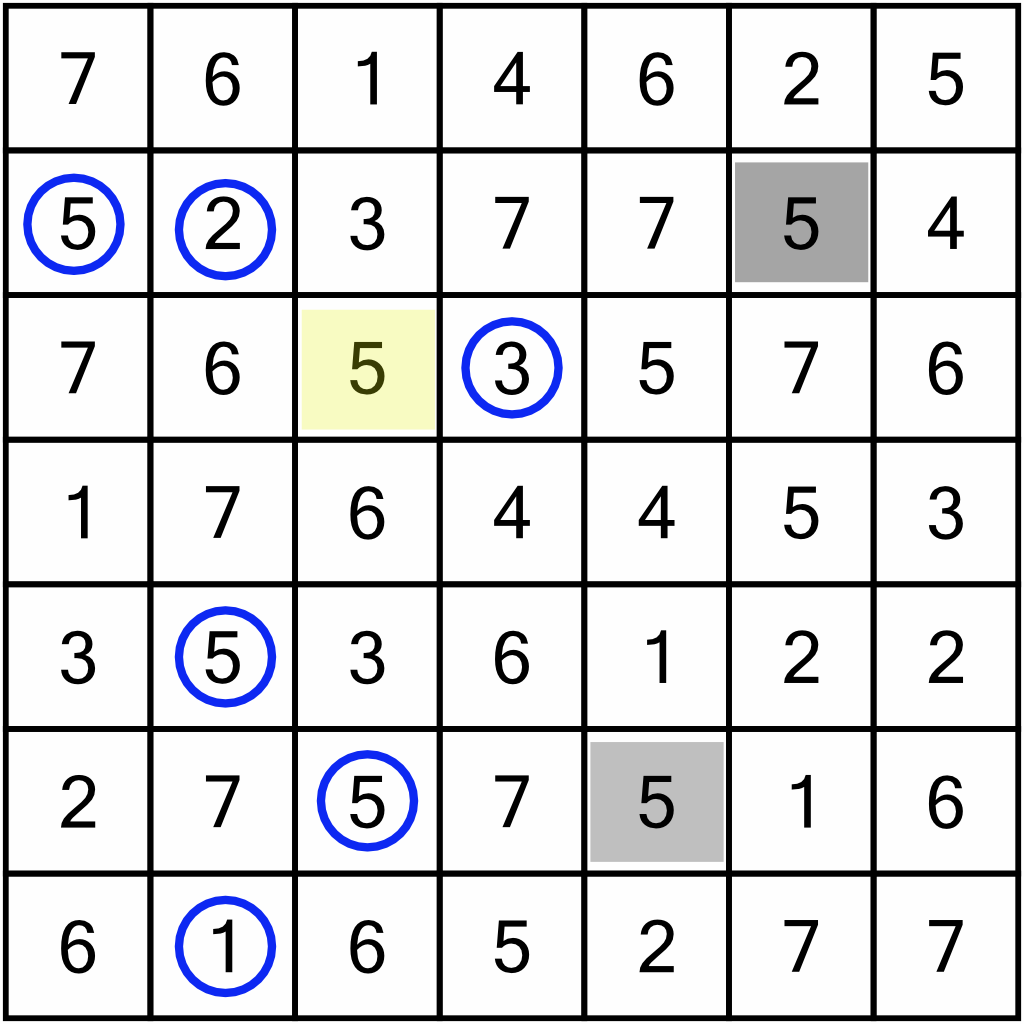
We’ll do the same for the columns. In column 3, there’s a duplicate 5, so that can be shaded in.

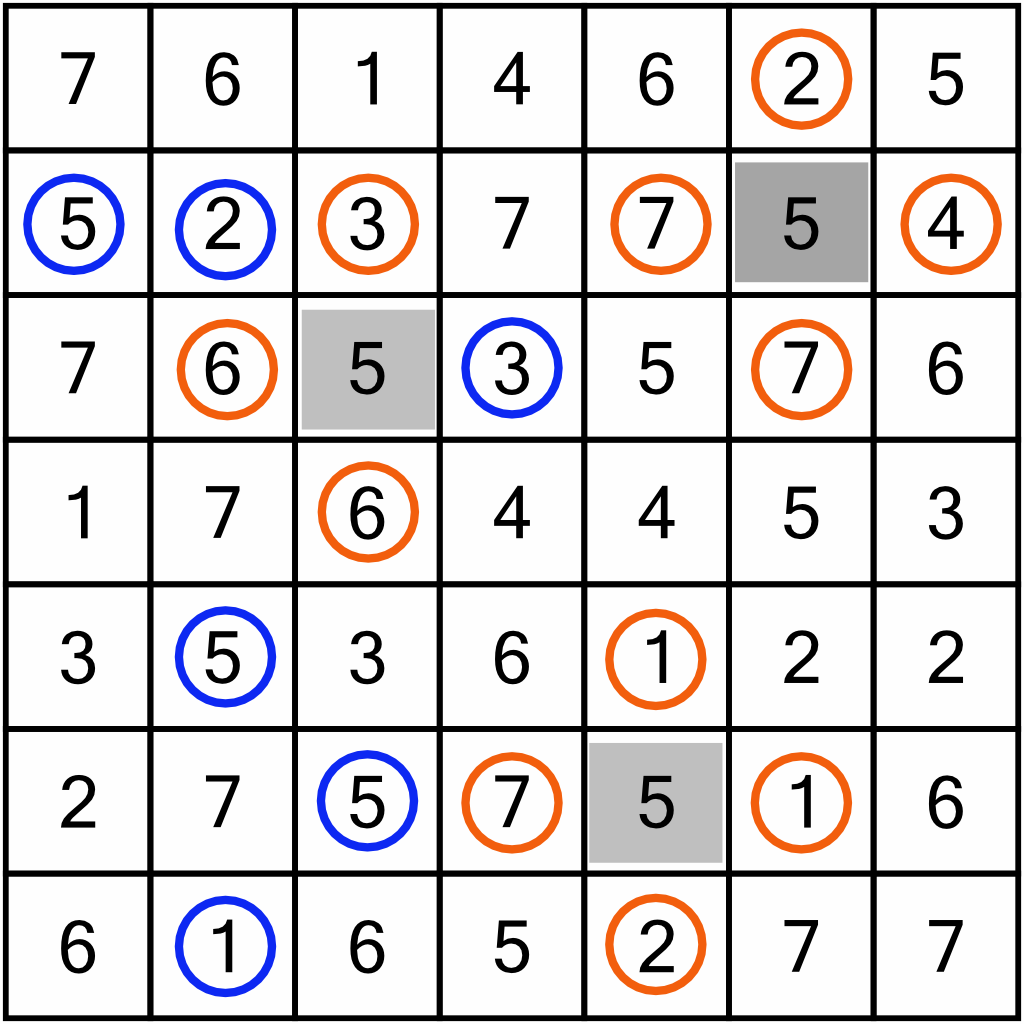
As we know that we can never have two shaded squares orthogonally adjacent, we can circle the digits immediately above, below, to the left, and to the right of those we have shaded in. They must be kept. We’ve circled these here in orange.

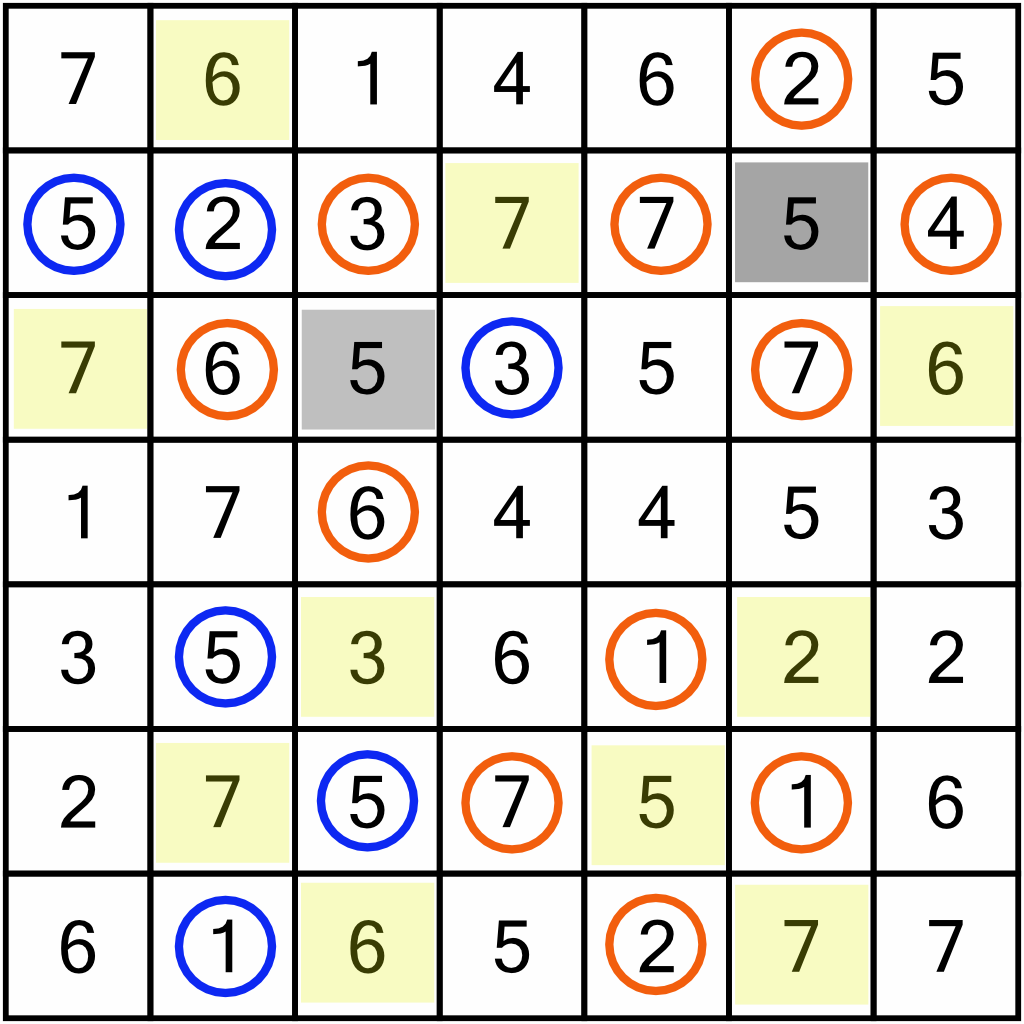
With eleven new circles on the board, we can go back through the rows and columns looking for duplicates we will be able to remove. For example, in column 2 we’ve a newly circled 6, so we can eliminate the duplicate 6 right at the top. Between all the rows and columns, that lets us eliminate ten new cells (shown here in yellow).

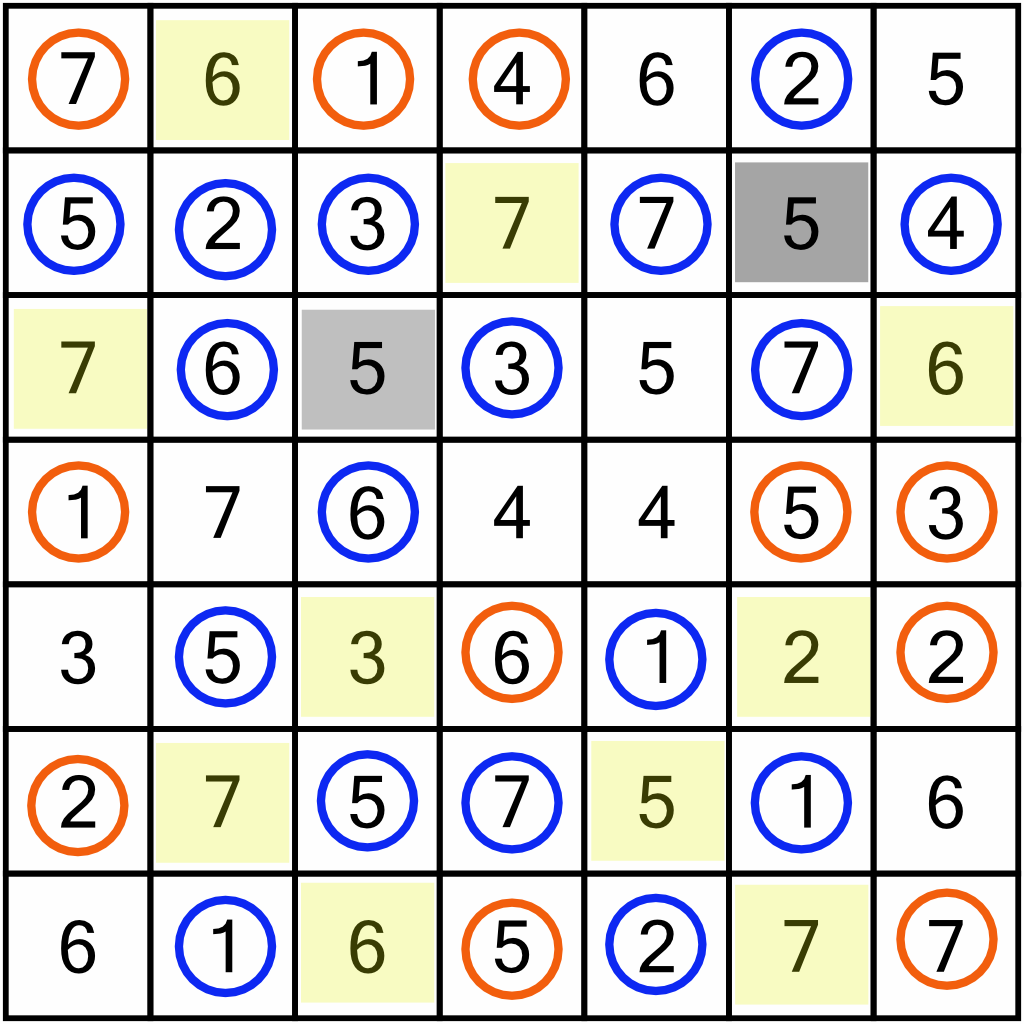
Now we repeat our earlier check, circling the cells above, below, and to the left and right of the newly eliminated ones. That gives us lots of new circles (shown here in orange)…

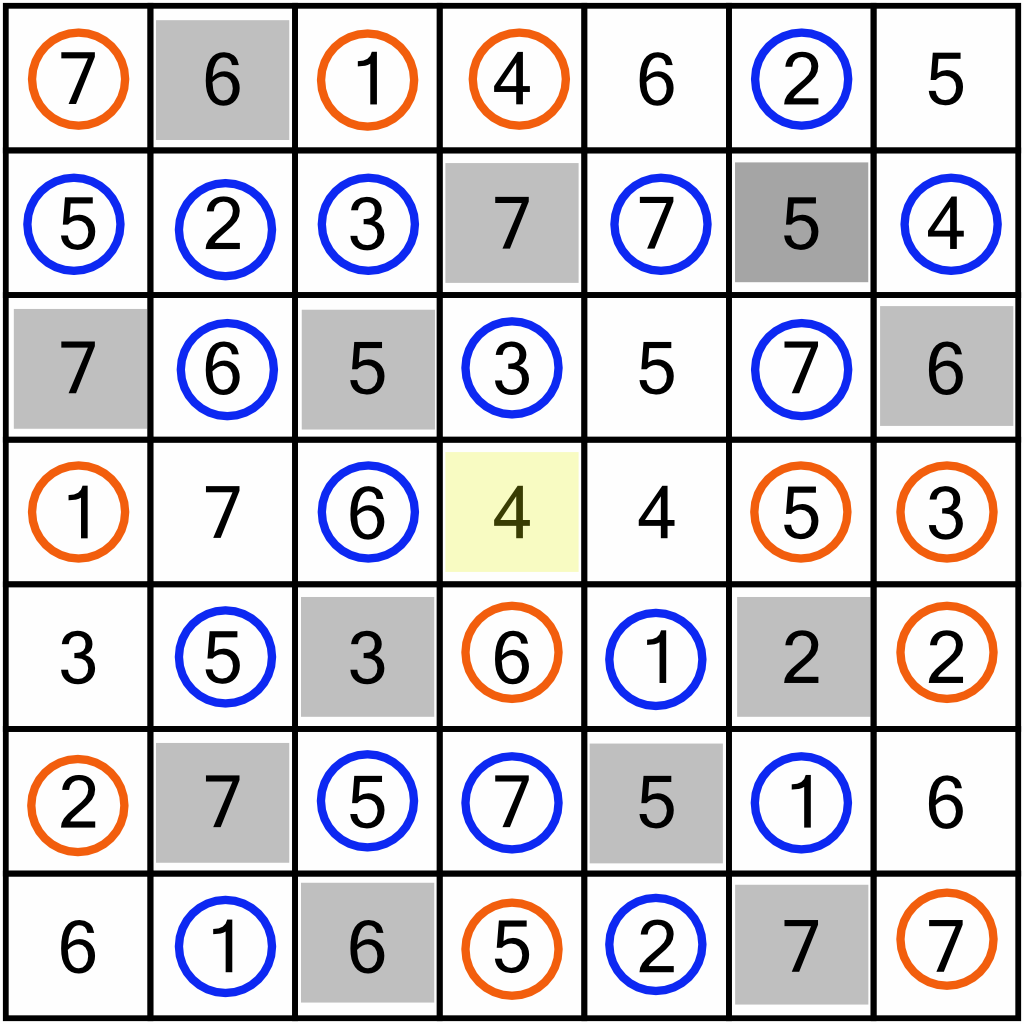
…and of course, we can use those to further eliminate doubles in the rows and columns. In fact, despite all those nice new orange circles, we can only eliminate one new cell – the 4 right in the middle.

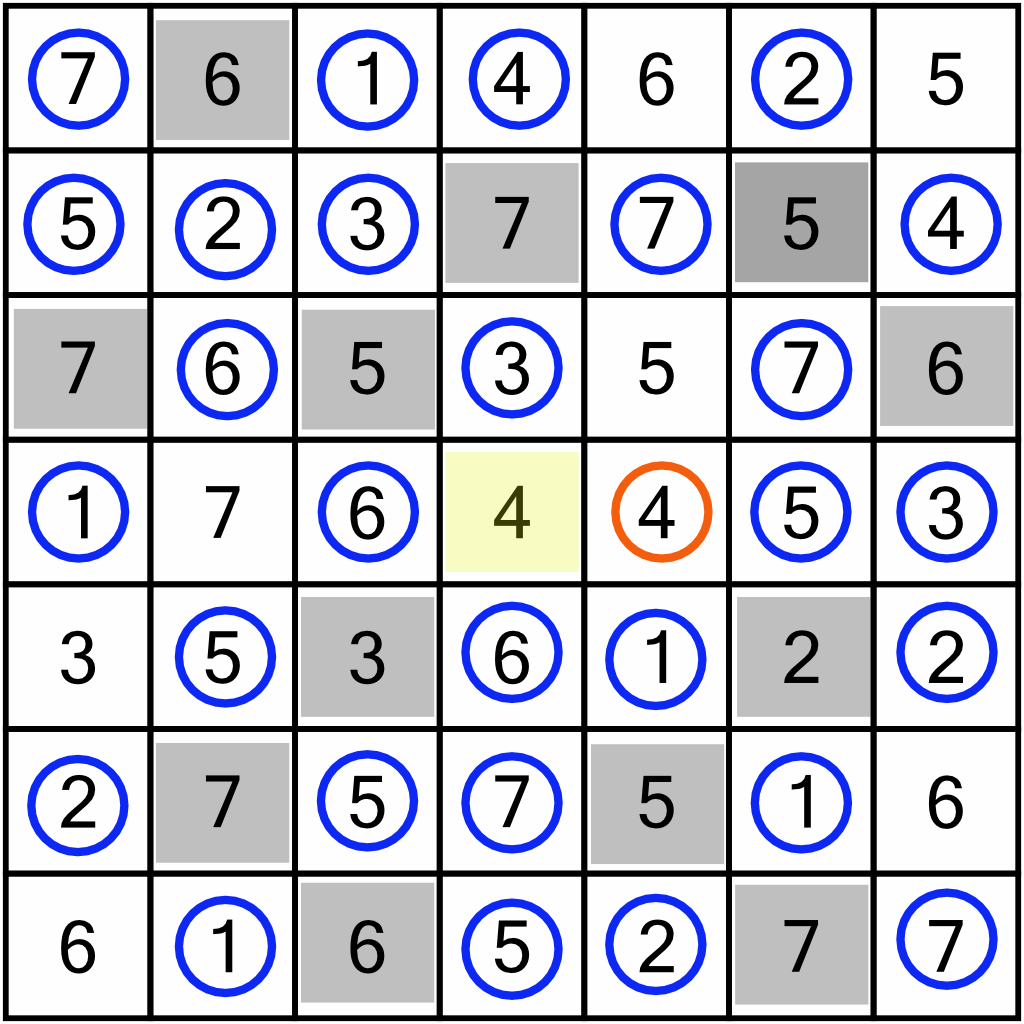
That 4 lets us circle the 4 immediately to its right.
We’ve reached a dead-end with the rippling of these eliminations; the four newly circled in orange don’t let us eliminate anything new, so where next? Let’s take stock of the board…remember, we only know that we’ve completed the puzzle once we are sure there are no duplicate numbers in any rows and columns.

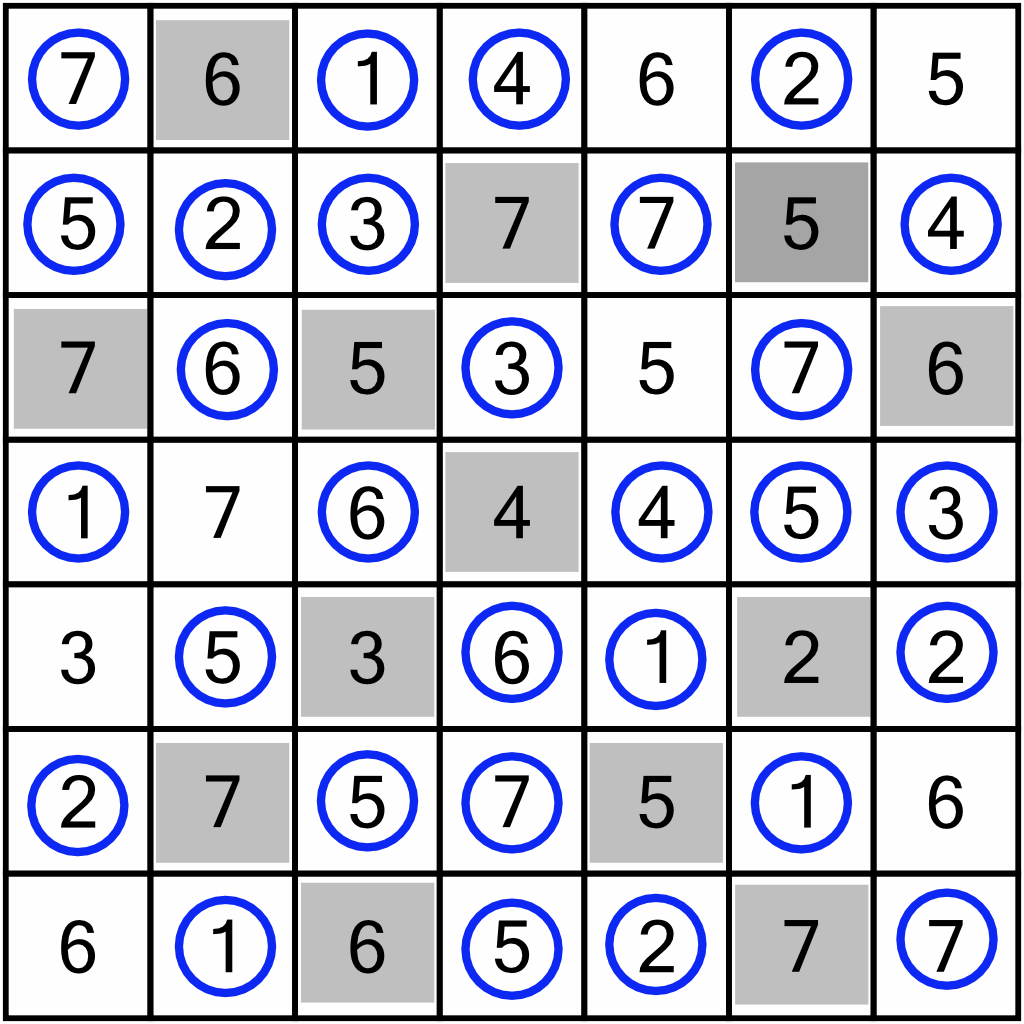
In fact, there are no more duplicates in any row or column, so we’ve completed the puzzle. I said it was an easy one!

Of course, being a Level 1 puzzle, that was pretty simple to solve. Everything rippled out and we could just use basic techniques. As puzzles get harder, you’ll need to take into account the rule about non-shaded cells making a single contiguous unit. Even harder puzzles will require chaining logic to determine which cells to keep and which to eliminate.

Try Hitori Yourself

Ready to try some puzzles yourself? We’ve put together a sample pack of four grids for you – a couple of easy ones, and a couple that are more challenging. Download the PDF below. Solutions are included so you can check your results.

Click Here To Download The Taster PDF

Where To Play

Ready for even more Hitori? We’ve got you covered!

Puzzle Weekly Presents: Hitori is a collection of 120 puzzles set over seven levels of difficulty. Grab a copy here.

Got a Kobo? We’ve got Hitori puzzles for that too! Hitori for Stylus Devices presents 100 puzzles over five levels, and is designed especially for Kobos with stylus. Find out more here.