Doors

This is the puzzle we are going to solve. It’s a small, easy puzzle. Smaller, in fact, than our usual Level 1 puzzles. But a regular puzzle would make this example too long and unwieldy, and a little puzzle is sufficient to see the solving techniques in action.

The first move is easy: as we have two 1s next to each other, we know there must be a door closed between them. If that door was open, then every other door surrounding those 1s would have to be closed, which would isolate them from the rest of the grid, and that’s not allowed by the rules. So this door must be closed.

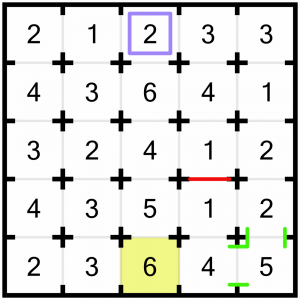
Now let’s turn our attention to this corner. Corners are obviously more constrained as they only have two doors. Why look at this corner in particular? Because it’s the largest number in a corner. We need to see five rooms, and we can only look up and to the left. Either direction will only show us a maximum of four rooms each (it’s actually fewer because the 1 in the vertical direction, and the 2 in the other corner, both ‘block’ us), so we know we are going to have to look at rooms in both directions if we are to meet the target. Therefore we know that both the doors to this cell must remain open. We can mark those in on the grid, so we know not to close them later.

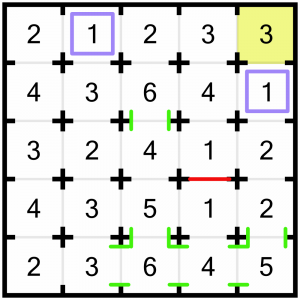
I’ve marked those doors open with the small green lines. We can do something similar here with this 6. At first glance, it looks like we can see a maximum of four rooms looking vertically (upwards). However, the 2 at the top of that column means we couldn’t open all the doors between it and the 6. We don’t know if the 2 will see any rooms in that column – it could see the 6 and the 4 below it, or just the 6, or nothing at all in that column. But we do know that we cannot have doors open all the way between our 6 at the bottom, and that 2. So the most rooms we can see vertically is three. That means to see our target of 6 rooms, we are going to have to leave all three doors open. Again, we’ll mark them in to remind us.

Let’s keep looking for forced openings. Another obvious place to look is this 6. Aside from the one we just looked at, it’s the biggest number on the board. However you look at it, we’re going to have to leave the bottom door open if we are to reach the target. There are various combinations in which one of the other three doors may or may not be closed, but we don’t know which is correct yet, so we’ll just mark in what we know for sure: that bottom door is going to have to stay open.

Now we’re going to have a look at this corner 3. Again, we’re rather constrained because we only have two doors. We are further constrained in that below that 3 is a 1, so if we leave the door between them open, we must close all other doors on the 1, shutting off that column as a source of rooms to view. We are further constrained by the 1 in the top row. If we left all the doors open between the 3 and the top 1, we would be fulfilling the criteria of the 3, but we would bust the 1 (it would be able to see 3 rooms!) These constraints, taken together, allow us to solve this cell. We must be able to see the two cells immediately to the left, and the cell below. We can draw in the openings, close the required doors, and strike through that 3 so we know we’ve solved it…

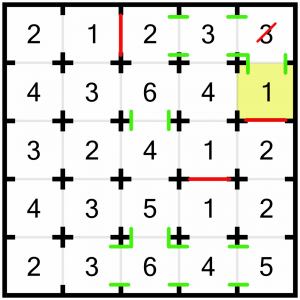
…like this. With the two doors we’ve closed, that 3 can now only see the required 3 rooms.
Closing those doors has some knock-on effects we need to deal with. Firstly, this 1. It’s looking at the 3, so we must close the remaining door to the left.

The 1 is completed so it can be struck off.
The 2 is also complete, because we can see the two threes to its right, as the interconnecting doorways are forced open. So we must close the remaining door, looking downwards.

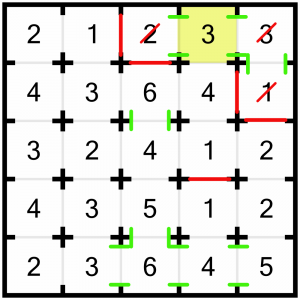
We’ve solved most of this top corner, but what about this 3? It can see two rooms (left and right), so it must keep its bottom door open to look at the 4, but it must not look any further. That means we have to close the bottom door of the 4.

With only one door remaining open, we can solve this 4. It can see one room above, so it must be able to see all three to the left. We’ll mark those doorways as open, and strike through the 4 as complete.

Looks like we’ve just solved this 6 into the bargain! We’ll mark the highlighted doorway between the 4 and the 5 as open.

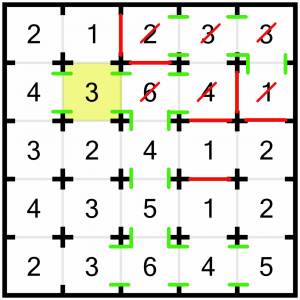
We can solve this 3, because with the open doors to the left and right it can already see three rooms. We need to stop it seeing any more, so have to close the top and bottom doors.

The 2 and the 1 can also be solved. The 1 already is – it’s only got one door left open! And the 2 must have its bottom door open, and we have to close the one beyond it (the bottom door of the 4)…

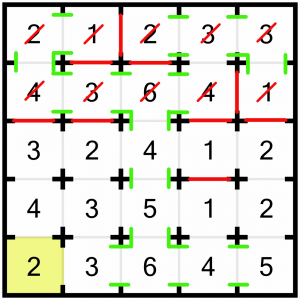
…which coincidentally also solves the 4.
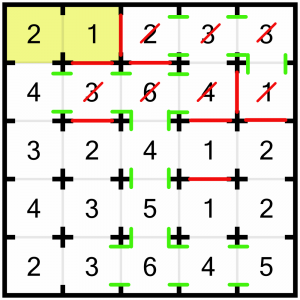
I’m going to return to the bottom of the puzzle now, and look at this 2 in the corner. If we leave the door to the right open, we’re going to have a problem as all the other doors further right must stay open and we’d see far too many rooms. So we must close the right-hand door, and we must force open the two doors to the top so we can see enough rooms.

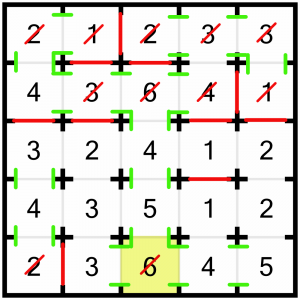
Not only has that solved that 2, it also completes this 6 because it’s now reached its target number.

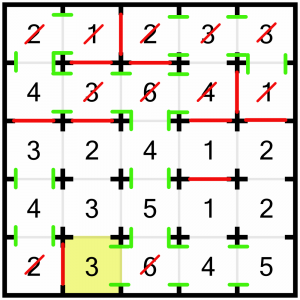
…and it lets us solve this 3 – we must close the top door.

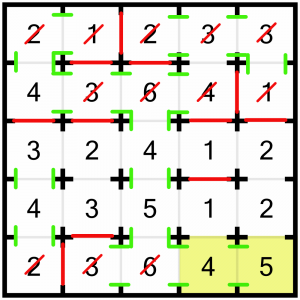
They’re dropping like flies now. The 4 is solved already. The fact it must open onto the 1 above it means we can shut the other doors on that 1 and mark it as complete.
The 5 is also solved, and we can mark the doors above it as open, which will help solve the other rooms.

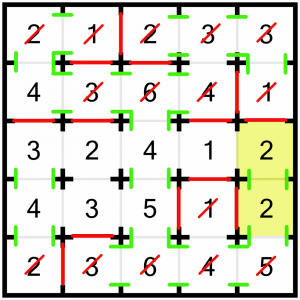
Both of these 2s are done, and we can close the other door on the top one.

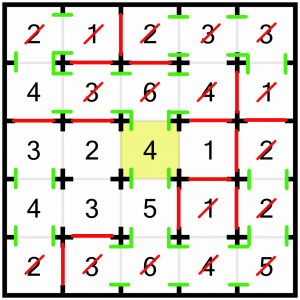
We can solve this 4, because we know the 1 to its right must open on to it. With the doors at the top and bottom of the 4 already forced open, it has reached its complement of visible rooms, so we can close the left-hand door.

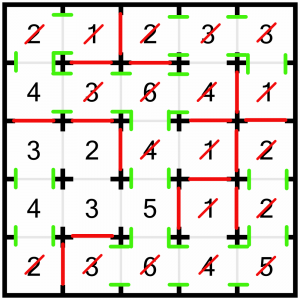
And that’s it! Even though we haven’t struck through them, all the other rooms are actually solved now.
It might look like it took a lot of effort to solve such a simple puzzle, but that’s because we broke it down into very small steps. As you get comfortable marking doors open and seeing where the forced openings then require doors to close, the puzzle flows beautifully. If you want to try some yourself, keep reading for some freebies…